Cheese Congress (practical task)
The Kazhakh Cheese Congress (KCC) hosts mice from different regions of the country. The regions are numbered from to . From each region , there will be visiting experts for sheep’s cheese and experts for goat’s cheese. The participants of the congress are traditionally hosted in two-bed rooms. is the sum of all such that all rooms are fully occupied. The rooms are numbered from to . To encourage communication, the Organizing Committee of the Kazhakh Cheese Congress (OCKCC) aims to split up the participants into rooms according to a certain scheme: In each room there should be hosted an expert for sheep’s cheese and an expert for goat’s cheese, and those two mice should be from different regions. Can you help the OCKCC to accomplish this task?
Subtask 1: Two Regions (10 points)
For this subtask it holds that , and your program should decide if there is a possible splitting. Input —– The first line of the input contains a single integer , the number of test cases. test cases follow. Each test case consists of a single line containing the two integers and , separated by a single space.
Output
For the -th of the inputs, print “Case #i:”, followed by “POSSIBLE” if splitting is possible and “IMPOSSIBLE” otherwise.
Constraints
- , i.e. there are exactly test cases
Examples
Input:
2 1 1 1 2
Output:
Case #1: POSSIBLE Case #2: IMPOSSIBLE
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: More Regions (30 points)
For this subtask, can take on other values, and your program should decide, if there is a possible splitting. Input —– The first line of the input contains a single integer . test cases follow. Each test case consists of a single line with the integer , describing the number of regions, followed by the numbers , separated by single spaces.
Output
For the -th of the inputs, print “Case #i:”, followed by “POSSIBLE” if splitting is possible and “IMPOSSIBLE” otherwise.
Constraints
- , d.h. es gibt genau Testfälle
Examples
Input:
2 3 2 1 1 3 4 2 1
Output:
Case #1: POSSIBLE Case #2: IMPOSSIBLE
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Explicit Scheme (40 points)
For this subtask, you program should print an explicit splitting of mice into rooms, if there is such a splitting. Input —– The first line of the input contains a single integer . test cases follow. Each test case consists of a single line with the integer , describing the number of regions, followed by the numbers , separated by single spaces.
Output
For the -th test case, print “Case #i: IMPOSSIBLE”, if there is no possible splitting. Otherwise print the line “Case #i:”, followed by lines, where the -th such line contains the integers and . Each of those lines describes the mice hosted in one of the two-bed rooms: The -th room hosts an expert for sheep’s cheese from region together with an expert for goat’s cheese from region .
There can be many different possible splittings. In this case, your program should print an arbitrary possible splitting.
Constraints
- , i.e. there are exactly test cases
Examples
Input:
3 4 1 1 1 1 3 2 1 1 2 1 2
Output:
Case #1: 1 3 2 1 3 4 4 2 Case #2: 1 2 2 1 3 1 1 3 Case #3: IMPOSSIBLE
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4: More Categories (20 points)
The OCKCC is thinking about inviting mice from each region, where . As the scheme, according to which the mice where splitted up into rooms has made a lot of sense so far, it should now be applied in a more general form. This means that for , this new scheme is identical with the previous scheme. From each region there will visit mice from different categories (like experts for sheep’s cheese, goat’s cheese, spicy cheese, mild cheese, …). The categories are numbered from to . Those mice should then be split up into -bed rooms such that in each room there are no two mice from the same region and no two mice from the same category. (In particular, in each room there is exactly one mouse from each category.) Input —– The first line of the input contains a single integer . test cases follow. Each test case consists of a single line with the integers and , the number of regions and the number of categories respectively, followed by the integers , separated by single spaces.
Output
For the -th test case, print “Case #i: IMPOSSIBLE”, if there is no possible splitting. Otherwise print the line “Case #i:”, followed by lines, where the -th such line contains integers . Each of those lines describes the mice hosted in one of the -bed rooms: Within the -th room, the expert of category is from region .
Constraints
- , i.e. there are exactly test cases
Examples
Input:
3 3 2 2 1 1 3 3 2 1 1 3 3 1 1 1
Output:
Case #1: 1 2 2 1 3 1 1 3 Case #2: IMPOSSIBLE Case #3: 3 1 2 1 2 3 2 3 1
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Word chain (practical task)
Mouse Stofl wants to compose some novel poems that consist of nice word chains. His fancy idea is that he wants to use words that occur inside other words.
A word occurs in another word if all its letters appear in the same order inside the other word. For example: “Bach” occurs in “belauschen” but not in “hab”.
Subtask 1: Two words (20 points)
At first. Stofl wants to compose a poem of length . To do this he wants to know for two words whether one occurs in the other. Help him answer this question.
Input
The first line contains the number , the number of poems that Stofl wants to compose. After that lines, each containing two words, follow.
Output
For each of the inputs you have to output a single line. Each line should start with “Case #i:”, followed by “YES”, if one of the two words occurs in the other and “NO”, if not.
Constraints
- Each word consists of at most small letters from a to z.
- , i.e. there are exactly poems.
Examples
Input:
3 bach belauschen belauschen bach bach dach
Output:
Case #1: YES Case #2: YES Case #3: NO
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: Short poems (30 points)
Stofl now has an entire list of words in front of him and tries to find two of them that build a poem. Determine whether there are two words in the list that build a poem.
Input
The first line contains the number , the number of poems that Stofl wants to compose. inputs follow, each of them structured like this: The first line contains the number . The next lines each contain a word .
Output
For each of the inputs you have to output a single line. Each line should start with “Case #i:”, followed by “YES”, if a poem of length exists abd “NO”, if not.
Constraints
- , i.e. there are at most different words.
- Each word consists of at most small letters from a to z.
- , i.e. there are exactly poems.
Examples
Input:
2 5 bach dachs belauschen obacht dach 4 bach dach fach sache
Output:
Case #1: YES Case #2: NO
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Long poems (50 points)
After Stofl mastered the art of short poems, he now tries to write longer ones. Each poem consists of one nice word chain. A word chain is nice if each word occurs in all subsequent words. “ah, bach, belauschen” is a nice word chain, because “ah” occurs “bach” as well as in “belauschen”, and “bach” occurs in “belauschen”. “ah, bach, brach, belauschen” on the other hand is not nice, because “brach” does not occur in “belauschen”.
Stofl wants to compose long poems and nice long word chains for that. Given a list of words, try to find the length of the longest word chain.
Input
The first line contains the number , the number of poems that Stofl wants to compose. inputs follow, each of them structured like this: The first line contains the number . The next lines each contain a word .
Ouptut
For each of the inputs, you have to output “Case #i:” followed by , the length (number of words) of the longest word chain.
Constraints
- , i.e. there are at most words and the solution is at most the number of words.
- Each word consists of at most small letters from a to z.
- , i.e. there are exactly poems.
Examples
Input:
2 8 bach dachs brach belauschen obacht ah belauschend dach 3 bach dach fach
Output:
Case #1: 4 Case #2: 1
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Audio (practical task)
Stofl is listening to a boring audio file. The talker speaks very slowly and Stofl wonders, if he might shorten the long sounds, in order to be done faster.
A “sound” is an interference of waves of different periods, resulting in a new wave with a longer period.
Stofl knows from his physics class, that the period of the resulting wave is given by the smallest common multiple of the single periods.
Subtask 1: Single Interference (20 Punkte)
Given periods , compute the period of the resulting wave for multiple test cases.
Input
The first line of the input contains the integer , the number of test cases. lines follow. Each line starts with an integer , the number of single waves. numbers up to follow, the single periods. Those are separated by single spaces.
Output
For the -th test case, print “Case #i:”, followed by the number , the resulting period.
Constraints
- It is guaranteed that
- i.e. there are exactly test cases
Examples
Input:
3 3 6 8 4 2 8 4 4 10 3 5 2
Output:
Case #1: 24 Case #2: 8 Case #3: 30
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: Multiple Interferences (40 Punkte)
Stofl is thinking that a single sound can be shortened most (while keeping its character), by only playing one period in full, and attaching just the remainder of the wave.
If therefore a (resulting) wave of period ms is playing for ms in total, it goes through full periods with a remainder of ms. (, with remainder ). The sound character would however be preserved by playing only one period and ms of the remainder, therefore the section could be shortened from ms to ms. Furthermore, Stofl only wants to hear relevant parts of the file. If a section of the file is completely silent, this section should therefore be removed from the file completely.
An audio file consists of single waves, having periods , a starting time and an ending time and interfere accordingly. Your task is to shorten multiple files as described above. The resulting audio files will consist of sections ( may differ for different files), in a certain order. Each section consists of a certain period and takes time . Note, that two subsequent sections having the same period cannot be combined into one. (Because generally, the sound in one section will not be the same as the sound in the other section.)
Input
The first line of the input contains the number , the number of files to be shortened. files follow: Each file is initiated by a line with the number , the number of single waves. The following lines describe a single wave each: They contain for each single wave the integers , and , the period, the starting time and the ending time of this single wave.
Output
You should print the resulting audio files as follows: The first line of the -th audio file contains “Case #i:”. The next line of a file contains two numbers , the number of sections of this file and , the time at which the first section starts. The following lines describe the sections in the order in which they will be played. One line consists of the two numbers and , i.e. the resulting period and the duration of the section.
Constraints
- For all single waves it holds that .
- It is guaranteed that .
- i.e. there are exactly files.
Examples
Input:
3 3 15 20 120 2 0 20 6 1 150 2 7 2 101 11 23 123 2 2 1 2 3 3 10
Output:
Case #1: 4 0 2 1 6 7 30 40 6 6 Case #2: 3 2 7 7 77 78 11 11 Case #3: 2 1 2 1 3 4
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Big Files and Big Periods (40 Punkte)
The task description for this subtask corresponds to the task description of subtask 2, but you do not have to print the entire file explicitly.
Rather, for the -th section of the file, print modulo , where and is the period of the -th section of the file. modulo corresponds to the positive integer remainder of the division of by . In other words, modulo , and if modulo , then there is an integer such that .
(The shortened durations are no longer of any importance.)
Input
The first line of the input contains the number , the number of files. files follow: Each file is initiated by a line with the number , the number of single waves. The following lines describe a single wave each: They contain for each single wave the numbers , and , the period, the starting time and the ending time of the single wave.
Output
The first line of the -th output contains”Case #i:”. The next line of a file contains the two numbers , the number of sections of this file and , the time at which the first section starts. The following lines describe the sections in the order, in which they are played. A line consists of the single number modulo , i.e. the resulting period modulo .
Constraints
- For all single waves, it holds that and .
- i.e. there are extactly files
Input:
1 4 1000000007 1 2 1000000008 1 4 1000000009 1 4 1000000010 3 4
Output:
Case #1: 3 1 0 2 3
Grading
Since the input file for this subtask is huge, we will correct this task by hand. In order to allow you to test your solution on small inputs, we still provide a judging system. Please note, that the automated response is not final and you will be awarded points (if any) only after the submission deadline.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Yurt (theoretical task)
The nomadic people in Kazakhstan often live in yurts. A yurt is a traditional, big, round tent. On your trip you discovered a big campground. It has spots, numbered from to . On each spot, exactly one yurt is located. Also the yurts are numbered from to , such that a yurt and a spot always go together. But the yurts got mixed up as they were assembled in a hurry in the middle of the night. Now not necessarily all yurts are standing on the spot with the same number. Your task is to sort the yurts, so that they are in the right order again. You can do this step by step, always tearing down, switching and reassembling two yurts in each step. You can never dismount more than two yurts at once, so only swap two yurts at a time. Your goal is to use as few swaps as possible to bring the yurts into the correct order.
This task consists of four subtasks, two practical ones (1, 2) and two theoretical (3, 4). For the practical subtasks you have to write a program that solves the task and you can test it directly on the site and get immediate feedback. For the theoretical tasks we expect an explanation and justification of your solution in text form. Try to convince you and us that your idea really works. Your solution for theoretical tasks does not have to contain a complete compilable program. A precise explanation for example with pseudo code is sufficient. Also analyze your runtime and memory complexity and justify why your program always terminates.
Subtask 1: Practical part with few yurts (20 points)
In this subtask the campground includes at most yurts. It is your task to bring them in the correct order with as few swaps as possible. Your output gets accepted if you need at most swaps for yurts. So your program does not necessarily need to act optimally. For instance, if the tents are already in sorted order at the beginning, it is ok to do no swaps at all or to perform a few dummy swaps back and forth. You will think about the fact that swaps are always sufficient in subtask 3.
Input
The first line contains the number , the number of test cases. The following lines each describe a test case. Each line starts with the number of yurts, followed by space-separated numbers, to , where is the number of the yurt, that is place on spot initially.
Output
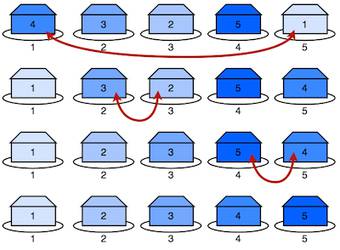
For each test case print one line with a possible sequence of or less swaps. For the -th test case start the line with “Case #t:”, followed by an even number of space-separated numbers . These numbers mean that in your -th swap the yurt on spot get interchanged with the yur on spot . (Example: means that the yurts on spot and get swaped. After that the yurts on spot and , and finally the ones on spots and ).
Constraints
- , so there are between and yurts.
- You are allowed to perform at most swaps.
- , so there are test cases.
Beispiele
Input:
2 3 1 3 2 5 4 3 2 5 1
Output:
Case #1: 2 3 Case #2: 1 5 2 3 4 5
Illustration of the second example:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: Practical part with many yurts (20 points)
In this subtask the campground includes at most yurts. It is your task to bring them in the correct order with as few swaps as possible. Your output gets accepted if you need at most swaps for yurts. So your program does not necessarily need to act optimally.
The format of the input and output is identical with subtask 1.
Constraints
- , so there are between and yurts.
- You are allowed to perform at most swaps.
- , so there are test cases.
Beispiele
Input:
2 5 4 3 2 5 1 10 10 2 3 4 5 6 7 8 9 1
Output:
Case #1: 1 5 2 3 4 5 Case #2: 2 3 3 4 2 4 3 4 1 10
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Theoretical part: at most swap (30 points)
The mouse Stofl now claims, that it is always possible to bring yurts with strictly less than (so at most ) swaps into the correct order. Describe how your algorithm solves this task and explain why you need less than swaps for every possible initial placement.
We expect you to explain and justify your solution as continuous text. Try to convince you and us that your idea really works. For this and the next subtask your submission does not necessarily need to include a complete compilable program. A precise explanation, e.g. with pseudo code, is enough.
The contest is over, you can no longer submit.
Subtask 4: optimal number of swaps (30 points)
You are not happy with just doing it in less than swaps, as for some initial placements it is possible to do it much faster. Can you argue for your algorithm that it acts always optimally? You should justify why every imaginable strategy needs at least as many swaps as yours.
The contest is over, you can no longer submit.
Note: You can implement and explain different approaches for the subtasks, if you want. If you find a solution for subtask 4 it is possible that you can use the same approach to solve the other subtasks as well.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
River (theoretical task)
In Kazakhstan there are some gigantic rivers. The river Irtysch for example is over kilometers long. It originates in China, flows through Kazakhstan and leads into the Ob in Russia. Along the Irtysch there are numerous cities. They are numbered from to . Each city has two districts, one on the left and one of the right side of the stream with a bridge that connects the two districts. Unfortunately, at a recent flooding all bridges collapsed.
To temporarily reestablish some connections across the river some ferries between given pairs of cities are planned. In order for the ferries to be able to land in the cities, each city has to construct exactly one dock. In each city, this dock can be built either on the left or each side of the city. Each city should have a dock, even if there is no ferry connection including it.
No new bridges across the river are planned. If one wants to cross the river one does have to use the ferry. In order for it to be as easy as possible to cross the river as many ferry connections as possible should cross the river, i.e. depart and land on different river sides. A ferry connection from city to city crosses the river for example, if the dock in is on the left and in is on the right side of the river. But if both docks are on the same side than this ferry does not cross the river.
Now the mayors of these cities have to decide on which side to construct their docks. Can you help them build their docks so that as many ferries as possible cross the river?
This task consists of a total of five subtasks, two practical (1a, 2a) and three theoretical ones (1b, 1c, 2b). For the practical subtasks you have to write a program that solves the task and you can test it directly on the site and get immediate feedback. For the theoretical tasks we expect an explanation and justification of your solution in text form. Try to convince you and us that your idea really works. Your solution for theoretical tasks does not have to contain a complete compilable program. A precise explanation for example with pseudo code is sufficient. Also analyze your runtime and memory complexity and justify why your program always terminates.
Subtask 1: Only river-crossing ferry connections (total 50 points)
In this first subtask we want to study the case when it is possible to choose the docks such that all ferry connections cross the river. To do this we first simplify the task by assuming the following: If one wants to travel from city to city only using ferries (independent of the river side at the start and end), then there is exactly one or zero ways to do this. This shall hold for every pair of cities and . This also includes indirect connections: If there is a connection from to and from to , you can for example assume that there is no direct connection from to but also no other city , that is connected to both and .
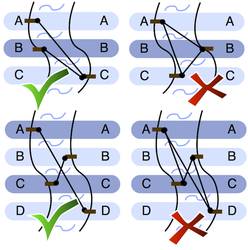
Subtask 1a: Implementation (20 points)
Can you write a program that constructs the docks under this simplification such that all ferry connection cross the river?
Input
The first line contains the number , the number of test cases. The following test cases are all formatted like this: one the first line there are the numbers and separated by a space, being the number of cities and the number of ferry connections . After that follow lines, each containing two space-separated numbers and , describing that there is a ferry connection from city to city .
Ausgabe
For each of the test cases output “Case #t:” followed by letters, each or . The letter -th of these letters indicates on which side the dock in city should get built.
Constraints
Examples
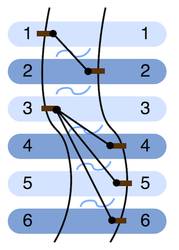
Input:
1 6 4 1 2 3 4 3 5 3 6
Output:
Case #1: LRLRRR
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 1b: Justification (15 points)
Please argue why your program from subtask 1a is correct? Why can you guarantee that always all connections cross the river? What is the runtime and memory complexity of your program?
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 1c: Relaxation of the condition (15 points)
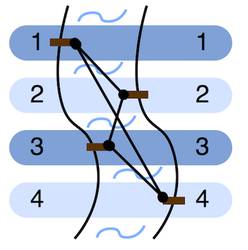
Your friend mouse stofl has found this new example and is surprised that it does not satisfy our condition from above (there are two paths from city to city , either directly or through the cities and ), but it is possible that all connections cross the river nevertheless.
Example
Input:
1 4 4 1 2 2 3 3 4 4 1
Output:
Case #1: LRLR
Can you find a better condition that describes exactly when it is possible that all ferry connections cross the river? Describe an algorithms that solves such instances and analyze it.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: at least half of it river-crossing (total 50 points)
Now let’s get rid off all conditions and let’s look at an arbitrary set of ferry connections. Mouse Stofle already found an example, where it is not possible to let all connections cross the river:
Example
Input:
1 4 4 1 2 2 3 1 3 2 4
Output:
Case #1: LRRL
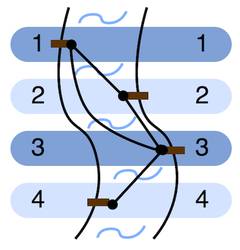
However you pick the docks at most three of the four connections will cross the river.
Stofl claims that it is possible to always pick the docks, such that at least half of all connections cross the river for any set of ferry connections. Is that really true? Can you find an algorithm that does that and can you argue why?
Subtask 2a: Implementation (20 points)
Write a program, that picks the docks such that at least half of all the ferry connections cross the river.
The format of the input and output is identical to subtask 1a.
Constraints
Example
Input:
1 5 10 1 2 1 3 1 4 1 5 2 3 2 4 2 5 3 4 3 5 4 5
Output:
Case #1: LRLRL
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2b: Justification (30 points)
Argue why your algorithm from subtask 2a is correct. Analyze its runtime and memory consumptions.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Note: You can implement and describe different approaches for each subtask if you want, of course.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Bazaar (creativity task)
This summer mouse Stofl was in Alamaty, the biggest city in Kasachstan. He was really impressed by the bazaar where he bought some diamonds. Those diamonds are sold using a special auction: every potential buyer chooses an amount of gold nuggets he wants to bid. The highest bid gets a diamond, but everyone has to pay their bid. To make it a bit more interesting and to prevent the richest from getting all the diamonds there is an additional rule: every person is only allowed to spend a given amount of gold nuggets during an auction.
Mouse Stofl will travel again to Alamaty to cheer for the swiss IOI team. He wants to visit the diamonds auction again. Help him to buy as much diamonds as possible with the allowed amount of gold nuggets.
The game
There are in total auctions. During each auction diamonds are auctioned. (This allows your program to analyze the strategies of the other programs and to develop a counter strategy). In each auction you have gold nuggets you are allowed to spend.
An auction consists of bid rounds. In each of those rounds each player bids covered his bid (i.e. the other players don’t know what your bid is). The player with the highest bid receives a diamond. If multiple players have the same highest bid then the diamonds will be sawed up resulting in one piece of the same size for every of those players. Every player has to pay their bid every round no matter who won. The sum of all bids of one player during one auction may not exceed .
Input / Output
Your program will be started by a game server. It has to read from stdin and output the moves to stdout.
On game start you receive one line with four space separated integers: , the number of players (incl. your program); , the number of auctions; , the number of bid rounds per auction (which corresponds to the number of diamonds); and , the number of gold nuggets per auction you are allowed to spend.
Afterwards auctions are played. In each there are bid rounds. A bid round looks like this:
1. You output an integer , the amount if gold nuggets you want to bid on the active diamond. 1. You receive one line with space separated integers, the bids of the other players for the active diamond. The order of the players stays the same during the whole game.
As soon as auctions were played your program should exit.
Examples
> 3 1 3 1000 < 100 > 20 80 < 50 > 70 80 < 25 > 120 80
Explanation: There are 3 players in total. In the first round you bid 100 gold nuggets, the other two players bid 20 and 80 gold nuggets respectively. You receive one diamond. After the three rounds each player owns one diamond.
Constraints
Evaluation
The evaluation for the creativity task is different from the one for the other tasks. You get
- 30 % of the points for a program which plays the game correctly i.e. it respects the rules and plays at least as good as the sample bots.
- Important: It is not allowed to simply submit the code of a sample bot. However it is allowed and recommended to use them as an example how to properly perform input/output in your programming language.
- The remaining 70% of the points will be rewarded according to the performance during the tournament on the SOI day.
So please optimize your program not only so that it wins against the sample bots, then we will also test it against the submissions of the other participants.
This year you are allowed to submit multiple programs (maximum 3 per participant) and your best program will be used for the ranking. Bundle these programs in a zip archive and submit that. The last submission counts for this task!
This year you are allowed to submit multiple programs (maximum 3 per participant, your last 3 submissions count) and your best program will be used for the ranking. We want to encourage you with this to implement riskier strategies as well as to try out several different strategies.
Hints
For interactive tasks it is important to flush the output buffer after every round to ensure that the server can see your output.
Use the following commands:
- C/C++: fflush(stdout);
- C++: cout << flush;
- Pascal: flush(output);
- There are similar commands in other languages.
Furthermore it is important that your program does not wait for more characters than the server provides you as input. Especially spaces and line breaks in C format strings are a frequent source of errors. For example if you read the last variable of the input with scanf("\%d ", &x);, the scanf function will wait for the next char which is not a space or a line break. However you will only receive such a char after you provided your next move. To solve this use instead scanf("\%d", &x); (no whitespaces after \%d).
Sample bots, server and visualization
During the first round we will provide the following material:
- sample bots in various programming languages.
- a server program you can use to let your program compete against itself or another program.
- a visualization to view simulated games.
You can download them here.
The contest is over, you can no longer submit.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Ranking
| Rank | Username | Total (600) | congress (100) | wordchain (100) | audio (100) | yurt (100) | river (100) | bazaar (100) |
|---|---|---|---|---|---|---|---|---|
| loading ... |