Alien Optimization

Written by Daniel Rutschmann. Translated by Daniel Rutschmann.

Contents

The Technique
Intuition behind the Technique
Degeneracy
Implementation

\newcommand{\kopt}{k_{\mathrm{opt}}} \newcommand{\ktask}{k_{\mathrm{task}}}

This article covers an advanced technique know as the “Alien trick”. The name originates from the task “Aliens” from IOI 2016, the task that made this technique popular. Other less popular names for this technique are “WQS/WPS binary search” or “Lagrange optimization”.

This article assumes that the reader is familiar with dynamic programming, greedy and scanline ideas. After all, you first need to come up with a correct solution before you can optimize it.

Suppose we are solving some minimization problem where we have some parameter $k$ that we need to keep in our state. Common examples of this are:

Splitting an array into exactly $k$ parts.
Picking exactly $k$ elements / edges / ranges.
Picking at most $k$ elements, but picking more elements is never worse.

In many cases, this parameter $k$ has to be kept as an additional dimension in our dp state, making our solution slower by a factor of $k$ . For instance, our solution might run in $O(n k)$ , but if we didn’t care about $k$ , we could get a solution with a runtime of $O(n)$ instead. The Alien trick allows you to get rid of the parameter $k$ under some convexity assumptions.

The Technique

For some minimization problem with some parameter $k \in \mathbb{Z}$ , let $f(k)$ denote the answer. A good example to think of is $f(k)=$ “minimal cost of splitting an array into $k$ parts”. To solve task, we want to compute the answer for some fixed $k = \ktask$ , i.e. we want to compute $f(\ktask))$ . Often, this is much more difficult than computing $\min_k f(k)$ (i.e. solving the problem without caring about the parameter $k$ ).

The alien trick applies to the case where $f$ is convex.

A function $f : \mathbb{Z} \to \mathbb{R}$ is convex if
$f(k+1) - f(k) \geq f(k) - f(k-1) \ \forall n \in \mathbb{Z}$
Some examples of convex functions are $f(k) = k^{2}$ or $f(k) = 2^k$ .

Instead of computing $f(\ktask)$ , the alien trick fixes some $\lambda \in \mathbb{R}$ and computes

\min_{k} (f(k) - \lambda k)

i.e. it doesn’t require the solution to have a correct values of $k$ , but it helps (if $\lambda > 0$ ) or penalizes (if $\lambda < 0$ ) solutions that have a large value of $k$ . Let $k_{\mathrm{opt}}(\lambda)$ denote the optimal value of $k$ for a certain $\lambda$ , i.e.

k_{\mathrm{opt}}(\lambda) = \arg\min_k (f(k) - \lambda k)

In our example, this would correspond to the number blocks we would use if every block has a cost of $-\lambda$ . The key observation is the following:

If $f$ is convex, then $k_{\mathrm{opt}}$ is non-descreasing. In other words, higher values of $\lambda$ will lead to higher values of $k_{\mathrm{opt}}$ .

This property allows us to binary search for $\lambda$ to find a solution for which $k_{\mathrm{opt}} = k$ . This allows us to replace the factor $k$ in the runtime with a log-factor from the binary search.

Intuition behind the Technique

Let $f : \mathbb{Z} \to \mathbb{R}$ be a convex function. If we plot a convex function, the graph looks like the bottom half of a convex polygon

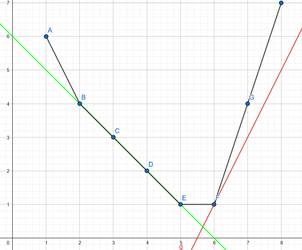
Computing $\min_k (f(k) - \lambda k)$ corresponds to finding a lower tangent with slope $k$ to this graph / polygon.

We can also see this mathematically. As $\kopt$ is the optimial $k$ , we have

f(\kopt) - \lambda \kopt \leq f(\kopt+1) - \lambda (\kopt+1)

i.e.

\lambda \leq f(\kopt+1) - f(\kopt)

Similarly, we have

f(\kopt) - \lambda \kopt \leq f(\kopt+1) - \lambda (\kopt+1)

i.e.

f(\kopt) - f(\kopt-1) \leq \lambda

The two equations

\begin{array}{rl} f(\kopt) - f(\kopt-1) &\leq \lambda\\ f(\kopt+1) - f(\kopt) &\geq \lambda \end{array}

tell us that the “slope” to the left of $\kopt$ is at most $\lambda$ and the “slope” to the right of $\kopt$ is at least $\lambda$ . Hence the line with slope $\lambda$ at $(\kopt, f(\kopt))$ is a tangent.

As $f$ is convex, the “slope” $f(k+1) - f(k)$ is non-decrasing in $k$ , hence higher values of $\lambda$ will lead to higher values of $\kopt$ .

Degeneracy

TODO

For (2), just interpolate linearly between the integer values of f. This will look something like this

Our interpolated function has corners, but we can still find the point (or segment in the case of the green line) where a line $g$ with slope $\lambda$ touches $f$ . Once again, increasing the slope of the line will make us find points further to the right, so we can binary search for $\lambda$ . The green line covers the one corner case we have to handle: If we’re looking for point $C$ or $D$ (i.e. $k = 3$ or $k = 4$ ), then we might only find $B$ and $E$ (i.e. we skip from $k=2$ to $k=5$ ). In the picture, we see that in this case we just linearly interpolate between $B$ and $E$ .

Implementation

To efficiently implement the Alien trick, we want to do everything with integers. Hence we will only use $\lambda \in \mathbb{R}$ .