Written by Benjamin Schmid and Bibin Muttappillil.
Contents
Wie die Dynamische Programmierung ist Scanline ein Muster zum Algorithementwurf und nicht ein einziges Problem. Ein Beispiel für ein Problem, das mit Scanline gelöst werden kann, ist die konvexe Hülle. Wir werden hier jedoch zwei einfachere Probleme betrachten, und an diesen die Funktionsweise von Scanline zeigen.
Es gibt auch ein paar video lectures zu diesem Thema:
Beispielproblem: Bananen im Schoggi-Fondue
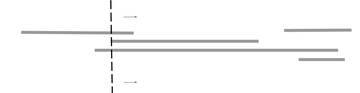
Wir betrachten (unterschiedlich lange) Bananen in flüssiger Schokolade in einem länglichen Gefäss, sodass die Bananen nicht nebeneinander Platz haben. Dafür können sie jedoch übereinander in der Schokoladen schwimmen. Genauer gesagt haben wir Strecken auf einer Linie gegeben, die sich überlappen können:

Nun haben wir eine Fonduegabel und möchten möglichst viele Bananen aufstechen. Dabei dürfen wir jedoch nur senkrecht einstechen:

Die Frage ist nun wie viele Bananen wir aufstechen können. Konkreter gesagt wollen wir herausfinden was das Maximum an Strecken ist, die sich überlappen.
Eine naive Lösung wäre für jede Teilmenge der Strecken zu schauen, ob sie einen gemeinsame Punkt besitzen und dann die grösste davon auszuwählen. Dieser Algorithmus würde jedoch in laufen, also extrem langsam. Glücklicherweise geht es um einiges schneller.
Algorithmus
Der Trick der Scanline ist nun, dass wir mit einer imaginären Linie über das Problem fahren und an interessanten Orten anhalten. An jedem dieser Haltepunkte wird nun eine oder mehrere geeignete Datenstrukturen aktualisiert. Wenn alle Haltepunkte abgearbeitet worden sind, kann aus den Datenstrukturen die Lösung bestimmt werden.
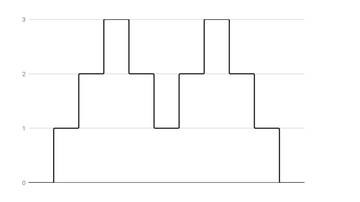
Wo sind diese interessanten Haltepunkte? Wir sehen, dass sich die Anzahl Strecken übereinander nur ändert, wenn eine neue Strecke anfängt bzw. eine alte aufhört. Somit sind Streckenendpunkte die Orte an denen wir unsere Antwort aktualisieren müssen.
Um diese Methode effizient auszuführen, können wir für jeden Anfangspunkt ein und für jeden Endpunkt ein in einer Liste einfügen und diese nach ihrer Koordinate auf der Linie sortieren.

Nun können wir durch die Liste iterieren und die Werte eins nach dem anderen aufaddieren. Unsere Lösung ist dann die grösste Zahl die erreicht wurde.
Implementierung
#include <iostream> //cin, cout #include <vector> //vector #include <algorithm> //sort, max using namespace std; #define int long long int scanline(vector<pair<int, int> > &segments){ vector<pair<int, int> > points; // add begin and end points for(auto s: segments){ points.push_back({s.first, 1}); points.push_back({s.second, -1}); } // note that endpoints are further to the front than beginpoints, if they happen to be on the same position. sort(points.begin(), points.end()); // iterate from left to right and find the maximum overlapping // adding +1 for every beginning of the banana and removing it (by adding -1) on the end int sol = 0; int cur = 0; for(auto p: points){ cur += p.second; sol = max(sol, cur); } return sol; } signed main() { ios_base::sync_with_stdio(false); cin.tie(0); // input int N; cin >> N; vector<pair<int, int> > bananas(N); for(int i = 0; i < N; i++){ int l, r; cin >> l >> r; bananas[i] = {l, r}; } cout << scanline(bananas) << "\n"; }
Laufzeitanalyse
Die Liste mit und zu erstellen braucht . Diese zu sortieren dauert dann . Das Iterieren am Schluss braucht wieder Zeit. Insgesamt läuft es also in . Beim Speicher haben wir nur die Liste, die jeden Anfangs- und Endpunkt besitzt, welches also gross ist. Die anderen Variablen sind unabhängig von und sind deswegen . Das führt dann zu Speicher insgesamt.
Beispielproblem: Billboards in New York
Wir betrachten einige achsenparalelle Rechtecke, die sich überlappen (z.B. die Skyline von New York). Für jedes Rechteck soll nun die Länge des von oben sichtbaren Teils der oberen Kante bestimmt werden (im Beispiel der Stadt z.B. um die Menge an Werbetafeln zu bestimmen).

Die naive Lösung dieses Problems wäre, für jedes Rechteck jedes andere Rechteck zu betrachten und dann die jeweils abgedeckten Bereiche abzuziehen. Damit aber Bereiche nicht doppelt abgezogen werden, müsste hierfür eine Liste mit den Bereichen, die übrig sind, gespeichert und durchsucht werden. Dies hat eine Laufzeit von , doch es geht besser. Schauen wir uns hierfür nun an, wie Scanline verwendet werden kann.
Algorithmus
Wir benutzen nun ein ähnlichen Trick wie vorhin mit der imaginären Linie. In den meisten Fällen ist die Linie horizontal oder vertikal und fährt dann entsprechend von oben nach unten bzw. von links nach rechts. Ebenfalls oft rotiert die Linie um einen Punkt (wie z.B. in manchen Implementationen für die konvexe Hülle).
Betrachten wir nun diese Methode an unserem Beispiel. Zuerst überlegen wir, in welche Richtung die Scanline verlaufen soll. Rotieren macht eher wenig Sinn, also wird es horizontal oder vertikal sein. Es ist beides möglich, doch wir werden die vertikale Linie wählen, da diese einfacher ist. In diesem Fall können wir jeweils zum aktuell zuoberst gelegen Rechteck (anhand der y-Koordinate der oberen Kante) die zurückgelegte Distanz hinzufügen. So haben wir am Ende für jedes Rechteck die gesuchte Länge aufaddiert.

Überlegen wir nun, was interessante Punkte sind. Während dem die Linie über ein Rechteck fährt, gibt es nichts zu tun. Es ändert sich nur etwas, wenn ein Rechteck beginnt oder aufhört. Wir wählen daher die linken und rechten Kanten als Haltepunkte. Um nun das bewegen der Linie zu simulieren, sortieren wir die Haltepunkte nach aufsteigender x-Koordinate und verarbeiten diese der Reihe nach. Beachte, dass wenn mehrere Punkte die selbe x-Koordinate haben können, du dir gut überlegen musst, welche du zuerst bearbeiten möchtest. In unserem Fall spielt es keine Rolle.
Als nächstes ist eine geeignete Datenstruktur gefragt. Dazu muss man sich fragen, was genau man jeweils an einem Haltepunkt bzw. am Ende wissen muss. In diesem Fall müssen wir am Ende für jedes Rechteck die sichtbare Länge wissen. Hierfür bietet sich ein Integer-Array an. An jedem Haltepunkt müssen wir das momentan oberste Rechteck wissen. So können wir die seit dem letzten Haltepunkt zurückgelegte Distanz zu diesem hinzufügen (da es das oberste ist, war es offensichtlich sichtbar). Da sich das oberste Rechteck zwischen den beiden Punkten nicht geändert haben kann (sonst hätte ja ein Rechteck anfangen oder aufhören müssen), addieren wir die Distanz zum richtigen Rechteck. Wir suchen also eine Datenstruktur, die uns erlaubt, schnell das oberste Element abzufragen, neue Elemente hinzuzufügen und zu entfernen. Hierfür eignet sich z.B. ein Heap [1] oder ein balancierter Baum. Dies musst du natürlich nicht selbst implementieren sondern kannst die Implementation in der C++ Standard Library verwenden: priority_queue für einen Heap, set für einen balancierten Baum.
Implementierung
#include <iostream> //cin, cout #include <vector> //vector #include <set> //set #include <algorithm> //sort using namespace std; #define int long long struct rect{ int x1, x2, y1, y2; int dist; } void scanline(vector<rect> &rects){ vector< pair<int, int> > points; // the first element is used to sort the list // the second is the index of the rectangle for(int i = 0; i < N; i++){ points.push_back({rects[i].x1, i}); points.push_back({rects[i].x2, i}); } sort(points.begin(), points.end()); // datastructure to hold the top rect // first element is the height, used to sort the set, highest height is in the beginning // the second is the index of a rectangle set< pair<int, int>, greater< pair<int, int> > > topRect; // this is the x-coordinate from the last stop the scanline made int lastPoint; for(auto p: points){ // get the current x-coordinate and rectangle int curPoint = p.first; int curRect = p.second; if(!topRect.empty()){ // get the highest rect if it exists int top = topRect.begin()->second; // add the distance the scanline travelled rects[top].dist += curPoint - lastPoint; } // update last point scanline visited lastPoint = curPoint; // update data structure holding rects if(curPoint == rect[curRect].x1){ //condition of beginning or ending of a rect topRect.insert({rect[curRect].y1, curRect}); }else{ topRect.erase({rect[curRect].y1, curRect}); } } } signed main() { ios_base::sync_with_stdio(false); cin.tie(0); //input int N; cin >> N; vector<rect> rects(N); for(int i = 0; i < N; i++){ cin >> rects[i].x1 >> rects[i].y1 >> rects[i].x2 >> rects[i].y2; } scanline(rects); //output for(rect r: rects){ cout << r.dist << " "; } cout << "\n"; }
Laufzeitanalyse
Die Laufzeitanalyse besteht aus zwei Teilen. Zuerst muss bestimmt werden, wie viele Haltepunkte bearbeitet werden. In unserem Fall sind das Haltepunkte, für jedes Rechteck genau zwei. Anschliessend muss noch die Laufzeit pro Haltepunkt bestimmt werden. In diesem Beispiel wird die Distanz berechnet (), diese zum obersten Rechteck hinzugefügt () sowie das Rechteck hinzugefügt () oder entfernt (). Pro Haltepunkt benötigen wir also . Somit ist die gesamte Laufzeit . Es ist jeweils zu beachten, dass das Sortieren der Haltepunkte ebenfalls benötigt.
| [1] | Hinweis für Fortgeschrittene: Da ein Heap Entfernen nur für das Maximum unterstützt, müssen wir einen kleinen Trick anwenden: statt ein Rechteck sofort zu entfernen, überprüfen wir bei jeder Anfrage nach dem Maximum, ob das Rechteck noch “aktiv” ist. Falls nicht, entfernen wir es jetzt. Da jedes Rechteck genau einmal eingefügt und einmal entfernt wird, ändert sich die (ammortisierte) Laufzeit nicht. |
Tasks
We recommmend you to solve the following tasks.
- servertest:
You need to log in in order to submit for this task.
Severtest is basically the same task as chocolate banana fondue.
- fishing:
You need to log in in order to submit for this task.
Fishing is a task similar to the chocolate banana fondue problem.
- drying:
You need to log in in order to submit for this task.
This is a task for those who look for a small challenge.