Overview
Welcome to the Second Round of the Swiss Olympiad in Informatics! You will find below an overview of what you’ve done so far as well as a few things that you should know before getting started.
This contest is over.
| Category | Task | Total | Subtask 1 | Subtask 2 | Subtask 3 | Subtask 4 | Subtask 5 | Subtask 6 | Subtask 7 |
|---|---|---|---|---|---|---|---|---|---|
| Junior only | registanpattern | ‒/100 | ‒/11 | ‒/17 | ‒/29 | ‒/43 | |||
| Junior only | timuridriders | ‒/100 | ‒/8 | ‒/9 | ‒/14 | ‒/18 | ‒/24 | ‒/27 | |
| Both | mousedances | ‒/100 | ‒/6 | ‒/12 | ‒/15 | ‒/13 | ‒/18 | ‒/14 | ‒/22 |
| Both | fire | ‒/100 | ‒/12 | ‒/19 | ‒/21 | ‒/22 | ‒/26 | ||
| Both | roborbuy | ‒/100 | ‒/10 | ‒/15 | ‒/10 | ‒/25 | ‒/40 | ||
| Both | bukhara | ‒/100 | ‒/7 | ‒/15 | ‒/18 | ‒/27 | ‒/33 | ||
| Regular only | tombexploration | ‒/100 | ‒/17 | ‒/18 | ‒/24 | ‒/41 | |||
| Regular only | evilruins | ‒/100 | ‒/6 | ‒/10 | ‒/19 | ‒/8 | ‒/14 | ‒/43 | |
| Regular only | 2h | ‒/100 | ‒/25 | ‒/25 | ‒/25 | ‒/25 |
Registan Pattern
Mouse Stofl and Mouse Binna have finally made it to Uzbekistan’s beautiful registans, which are full of colorful patterns.

Stofl found similarities in the patterns of the registan and he became artistically inspired! Although this time, Stofl had a way too crazy idea.
They came to a wall which is one meter tall and several meters long. The inspiring characteristics of the wall was its modular design every meter. Stofl’s idea was to cut the wall into one meter parts in order to rearrange them, which results in a new but still continuous pattern. However, Binna disliked his idea very much. She doesn’t care about the building itself, but she doesn’t like the lack of innovation. She thinks just rearranging the patterns is boring, so she gave him the challenge to make a unique pattern by dividing the wall into segments of several meters and then flipping all the segments in place.
However, Stofl has already assigned for each meter the position it should go. To impress Binna, he needs to find out how he can divide the wall such that he achieves his original vision by flipping the segments.
Subtask 1: A short wall (11 points)
Stofl has a wall which is meters long. Can you help him determine how he should divide the wall?
Input
The first line contains the number of test cases . For every test case, two lines will follow:
- The first line contains the integer , the length of the wall in meters.
- The second line contains integers for , describing Stofl’s assignment. The -th meter of the wall should move to the -th meter.
Output
For the -th test case, if it is not possible to achieve Stofl’s assignment by flipping segments, print “Case #t: Impossible”. Otherwise, print “Case #t: Possible” and two additional lines:
- The first line contains the number of segments .
- The second line contains integers , where is the length of the -th segment.
Limits
- for all , all are distinct
Example
Input:
2 3 0 2 1 3 2 0 1
Output:
Case #0: Possible 2 1 2 Case #1: Impossible
Solution for Case #0:
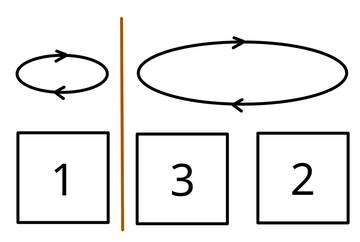
Dividing the wall into these two segments achieves that each meter of the wall ends up where Stofl wants it. Meter 1 is flipped by itself and thus remains where it is, while meters 2 and 3 are swapped.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: The entrance (17 points)
The walls at the entrance are up to meters long! Can you still help Stofl?
Input
Same as subtask 1.
Output
Same as subtask 1.
Limits
- for all , all are distinct
Example
Input:
3 3 1 0 2 5 1 0 4 3 2 6 2 1 5 4 3 0
Output:
Case #0: Possible 2 2 1 Case #1: Possible 2 2 3 Case #2: Impossible
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: All the walls (29 points)
The registan is huge! Despite that, the patterns have still the same characteristics everywhere. Stofl would be overjoyed if you could help him out on this ambitious task.
Input
Same as previous subtasks.
Output
Same as previous subtasks.
Limits
- for all , all are distinct
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4: All the registans (43 points)
Binna wasn’t impressed so far. So if this didn’t impress Binna, surely he needs to go even bigger than that and combine all walls of every registan in Uzbekistan.
Input
Same as previous subtasks.
Output
Same as previous subtasks.
Limits
- for all , all are distinct
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Timurid Riders
During the late Middle Ages, Uzbekistan was the heartland of the Timurid Empire, stretching from central Anatolia all the way to northern India, with Samarkand as its capital.
Binnas Birthday is coming up, and Mouse Stofl wants to prepare a special surprise for her. He knows that she is fascinated by the history of the Timurid Empire, and that she loves puzzles. So he came up with a puzzle based on the Timurid Empire.
The Timurid Empire in the puzzle consists of villages, including the capital, and roads between them, on which riders can travel. The capital Samarkand is always village . The villages bordering the wilderness have watchtowers to guard the borders. These villages can be recognized because they have exactly one road leading out and are not the capital. All other villages, including the capital, contain fortresses.
The puzzle further follows these rules:
- Riders may only be dispatched from the villages with watchtowers.
- Each rider travels only inward, toward the capital, never outward.
- Each rider continues travelling until it has reached the capital or the next village is already occupied.
- A new rider may only be dispatched once the previous rider has reached its final destination.
The goal is to decide from which watchtower to release each rider, and in what order, so that every fortress in the empire is manned in the least possible total time.
Stofl asked you to solve the puzzle, so that he can see if it is fit for Binna.
Subtask 1: Orders of Samarkand (8 points)
To test your understanding of the rules, Mouse Stofl wants you to predict which fortress each rider will stop at, given a list of dispatch orders.
Input
The first line contains the number of test cases . test cases follow in the following format:
- The first line contains the integer , the number of villages (with watchtowers or fortresses).
- Each of the following lines contain the integers , meaning there is a road from village to village which takes hours to ride on.
- The next line contains the integer , the number of riders which will be dispatched.
- The next line contains integers, , the cities with the watchtowers from which the riders will be dispatched (in this order).
Output
For the -th test case, output a line “Case #i: r_0 r_1 ... r_{M-1}”, where is the city in which rider will halt.
Limits
There are test cases. In each test case we have:
- for all
Example
Input:
3 3 0 1 0 2 2 1 2 3 0 5 1 3 3 2 2 2 6 4 1 0 1 2 3 0 2 2 5 3 3 1 3
Output:
Case #0: 0 2 Case #1: 0 1 2 Case #2: 0 4 2
Comment:
Disclaimer: Generation may take a few seconds.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: Caravan Trail to Samarkand (9 points)
Being satisfied that you understood the rules, Mouse Stofl will first give you an easier version of the puzzle, taking place along a caravan trail from the furthest away village all the way to Samarkand. In this version, there is exactly one capital and one village with a watchtower. All other villages have exactly one road leading in and one leading out.
Input
The first line contains the number of test cases . test cases follow in the following format:
- The first line contains the integer , the number of cities and watchtowers combined.
- Each of the following lines contain the integers , meaning there is a road from village to village which takes hours to ride on.
Output
For the -th test case, output a line “Case #i: K”, where is the minimum total time required to man every fortress.
Limits
There are test cases. In each test case we have:
- for all
Note: You may exceed the maximum recursion depth.
Example
Input:
3 3 0 1 1 2 2 0 5 4 0 3 1 2 2 4
Output:
Case #0: 5 Case #1: 5 Case #2: 19
Comment:
Disclaimer: Generation may take a few seconds.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Equal Roads of Bukhara (14 points)
Next, Mouse Stofl gives you a map centered around Bukhara. The unique feature is that all roads have length .
Input
Same as Subtask 2
Output
Same as Subtask 2
Limits
There are test cases. In each test case we have:
- for all
Example
Input:
3 3 0 1 0 1 4 0 1 3 1 0 1 6 4 1 0 1 2 1 0 1 2 1
Output:
Case #0: 1 Case #1: 2 Case #2: 4
Disclaimer: Generation may take a few seconds.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4: Balanced Roads of Shahrisabz (18 points)
In this subtask, Mouse Stofl gives you a map of the surroundings of Shahrisabz. The unique feature is that the capital has the same distance to every watchtower.
Input
Same as Subtask 2
Output
Same as Subtask 2
Limits
There are test cases. In each test case we have:
- for all
Example
Input:
3 3 0 3 0 3 4 0 3 3 2 0 1 6 4 1 0 1 2 2 0 2 2 2
Output:
Case #0: 3 Case #1: 5 Case #2: 6
Disclaimer: Generation may take a few seconds.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 5: A Province of the Realm (24 points)
In this subtask, Mouse Stofl gives you a map of a small portion of the Timurid Empire, with a small number of villages and roads.
Input
Same as Subtask 2
Output
Same as Subtask 2
Limits
There are test cases. In each test case we have:
- for all
Example
Input:
3 3 0 1 0 2 2 0 5 6 4 1 0 1 2 3 0 2 2 5
Output:
Case #0: 1 Case #1: 5 Case #2: 7
Comment:
In the first testcase, it is best to dispatch the first rider from the watchtower in city , who will ride to village in hour.
In the second testcase, there is only one option: dispatching a rider from the watchtower in city .
Disclaimer: Generation may take a few seconds.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 6: The Empire of Timur (27 points)
Mouse Stofl is now confident that you can solve the original puzzle with a map of the entire Timurid Empire.
Input
Same as Subtask 2
Output
Same as Subtask 2
Limits
There are test cases. In each test case we have:
- for all
Disclaimer: Generation may take a few seconds.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Mouse Dances
Mouse Stofl and friends are hosting a grand dance festival. All through the night, mice gather next to each other holding paws with their neighbors, swaying to the music, spinning in step, and pausing now and then for a nibble of cheese before the next melody begins.
But dancing is not always easy. When neighbors differ too much in height, their little paws strain with effort, their backs stretch or stoop too much and before long the mismatched neighbors grow tired and let go. The greater the height difference, the greater the inconvenience — and the sooner the dance floor empties.
To keep the celebration alive until sunrise, the mice must choose their places wisely: arranging themselves so that the maximum inconvenience between any two neighbors is as small as possible. Depending on the melody, they may form a line, gather in a circle, or even whirl apart into two circles — but always with the same goal: minimize the maximum inconvenience, and keep the dancing going through the night.
For each subtask, help Stofl arrange the mice for a different melody so that he can minimize the maximum inconvenience between neighbors.
Input
All subtasks use the same input format:
The first line contains the number of test cases . For each test case you get two lines:
- The first line contains a single integer — the number of mice.
- The second line contains integers: the heights of the mice .
For all subtasks we have , and .
Output
For the -th testcase, output a single line containing “Case #t: x” where is the smallest possible maximum inconvenience. For a given arrangement, the maximum inconvenience is defined as the maximum absolute difference between heights of adjacent mice. Then you may need to output additional lines depending on the subtask. (see each subtask’s “Output format”). When an arrangement is requested, it must be a permutation of the input heights.
Subtask 1: Tiny line (6 points)
The first melody is danced in a line. Help Stofl arrange a few mice in a line so that the maximum inconvenience is minimized.
Limits
Output format
Output two lines per test case: 1. A single integer — the minimal possible maximum inconvenience. 2. integers — a valid optimal arrangement (the order in the line).
Example
Input:
2 2 2 1 3 1 5 2
Output:
Case #0: 1 2 1 Case #1: 3 1 2 5
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: Medium line (12 points)
The second melody is also danced in a line. Help Stofl arrange a larger group of mice in a line so that the maximum inconvenience is minimized.
Limits
Output format
Output two lines (same as Subtask 1).
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Huge line (15 points)
The third melody is also danced in a line and it is such a popular song that not just Stofl’s village but several other villages march into the dance floor to join in. Help Stofl arrange a huge crowd of mice in a line so that the maximum inconvenience is minimized. To keep output small, output only the optimal value of inconvenience and not the actual arrangement.
Limits
Output format
Output one line containing a single integer — the smallest possible maximum inconvenience.
Example
Input:
2 2 2 1 3 1 5 2
Output:
Case #0: 1 Case #1: 3
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4: Medium circle (13 points)
The fourth melody is danced in a circle, so that the last mouse is a neighbor of the first mouse. Arrange the mice so that the maximum inconvenience is minimized.
Limits
Output format
Output two lines: 1. A single integer — the minimal possible maximum inconvenience on the circle. 2. integers — a valid optimal circle order (print in a list; wrap-around is implied between last and first mouse).
Example
Input:
2 2 2 1 6 8 5 6 10 10 9
Output:
Case #0: 1 2 1 Case #1: 3 5 8 10 10 9 6
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 5: Huge circle (18 points)
The fifth melody is also danced in a circle, with a huge crowd of mice dance joining in. Arrange the mice optimally, and to keep output small, output only the optimal value of inconvenience and not the actual arrangement.
Limits
Output format
Output one line containing a single integer — the minimal possible maximum inconvenience.
Example
Input:
2 2 2 1 6 8 5 6 10 10 9
Output:
Case #0: 1 Case #1: 3
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 6: Two medium circles (14 points)
To dance the sixth melody, the mice split into two circles, both non-empty. Arrange the mice in a way that minimizes the maximum inconvenience seen across the two circles.
Limits
Output format
Output four lines: 1. A single integer — the smallest possible maximum over the two circles’ maximum inconvenience values. 2. Two integers: — lengths of the two circles (both , ). 3. integers — a valid arrangement for the first circle 4. integers — a valid arrangement for the second circle
Example
Input:
2 2 2 1 7 8 5 6 10 10 9 1
Output:
Case #0: 0 1 1 2 1 Case #1: 3 6 1 5 8 10 10 9 6 1
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 7: Two huge circles (22 points)
For the seventh melody, a huge crowd of mice split into two circles, both non-empty. Arrange them in a way that minimizes the maximum inconvenience seen across the two circles. To keep output small, output only the optimal value of inconvenience and not the actual arrangement.
Limits
Output format
Output one line containing a single integer — the smallest possible maximum over the two circles’ maximum inconvenience values.
Example
Input:
2 2 2 1 7 8 5 6 10 10 9 1
Output:
Case #0: 0 Case #1: 3
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Fire
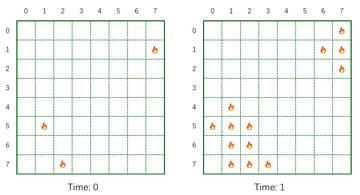
Mouse Binna is on an adventure in a vast forest that is modeled as an grid. Lately, the weather has been extremely dry, and the forest is about to catch fire. Binna is located at the top-left corner of the grid , while an underground shelter lies at the bottom-right corner , offering safety from the fire.
At time , fire starts in distinct cells of the grid — these are called fire sources. At each unit of time, the fire spreads:
- any cell that is currently on fire will remain on fire, and
- its direct neighbors (up, down, left, right) also catch fire.
Binna wants to know the latest time such that a safe path exists from her current location to the underground shelter . Both endpoints and all cells on the path must not be on fire at time . Moves are allowed only in the directions: up, down, left, right. If no such path exists even at time , then .
Subtask 1: Single fire source (12 points)
At time , there is exactly one fire source.
Input
The first line contains the number of test cases . test cases follow in the following format:
- The first line contains two integers , , representing the size of the grid and the number of fire sources.
- Each of the next lines contains two integers and — the row and column of a fire source.
Output
For each test case, output a line “Case #i: L”, where represent the latest time such that there still exists a safe path, or if no safe path exists even at time .
Limits
There are test cases. In each test case we have:
- for all
Example
Input:
3 7 1 1 3 4 1 2 1 4 1 1 1
Output:
Case #0: 2 Case #1: 1 Case #2: 0
Comment:
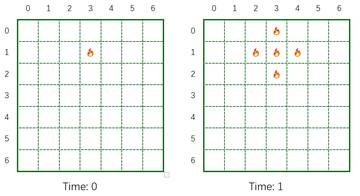
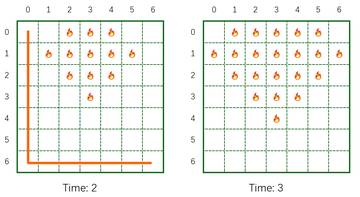
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: Aligned fire sources (19 points)
All fire sources are in the same row.
Input
Same as Subtask 1
Output
Same as Subtask 1
Limits
There are test cases. In each test case we have:
- for all
- for all
Example
Input:
2 7 3 4 0 4 1 4 3 20 2 15 2 15 6
Output:
Case #0: 2 Case #1: 12
Comment:
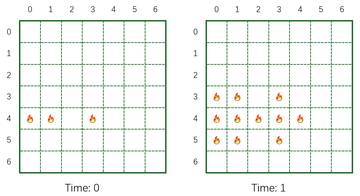
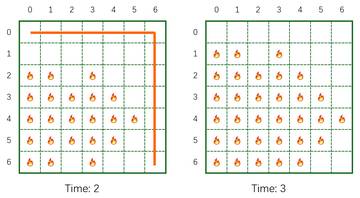
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Small grid (21 points)
The grid size is small.
Input
Same as Subtask 1
Output
Same as Subtask 1
Limits
There are test cases. In each test case we have:
- for all
Example
Input:
3 8 3 1 7 5 1 7 2 7 3 3 4 0 2 6 3 4 4 2 0 2 1 1 2 1 3
Output:
Case #0: 3 Case #1: 1 Case #2: -1
Comment:
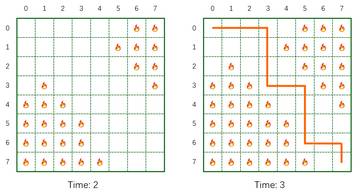
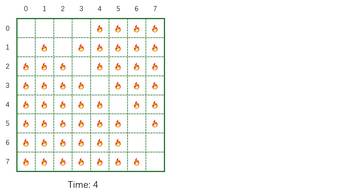
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4: Few fire sources (22 points)
The number of fire sources is small.
Input
Same as Subtask 1
Output
Same as Subtask 1
Limits
There are test cases. In each test case we have:
- for all
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 5: More fire sources (26 points)
Both the grid size and the number of fire sources are large.
Input
Same as Subtask 1
Output
Same as Subtask 1
Limits
There are test cases. In each test case we have:
- for all
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Rob or Buy
The Silk Road in Uzbekistan was a trade route, where merchants travelled to cities like Samarkand to exchange silk, spices and other goods. The many markets and caravans made it a center of commerce across Uzbekistan and other parts of Asia. It was a lively road with a lot of merchants and travelers, but also thieves and robbers!
On the road, there are merchants in a line, numbered from to . Each of them sells some goods. The goods of the -th merchant cost mouse coins. There is the myth of the “Silk Road’s great heist” in which the entire road was robbed in lightning speed! That’s why the merchants on the road created an alarming network to notify other merchants of an ongoing robbery. Each merchant is assigned a direction which is either for left, or for right. After a merchant is robbed, he will notice the robbery and alarm every merchant on his left or right respectively. Any merchant that is alarmed this way will pay extra attention and robbing the merchant becomes impossible.
Mouse Stofl wants to do the thievery himself and wants to get all the goods sold on the Silk Road. But since it’s impossible to steal from alarmed merchants, he will need to buy some of the goods. So the questions is, what is the minimum amount of money he needs to spend, if Stofl robs and buys the goods in the perfect order?
Subtask 1: The road between Samarkand and Bukhara (10 points)
Input
The first line contains the number of test cases . For each test case you get three lines:
- The first line contains the number of merchants .
- The second line contains the string where is either or , indicating the direction of the -th merchant.
- The third line contains spaces integers , indicating the price of the goods of the -th merchant.
Output
For each test case, output a line Case #i: P, where is the minimum amount of money Stofl needs to spend to get all the goods.
Limits
There are test cases. For each test case, we have:
- for all
Example
Input:
2 2 rl 3 5 3 lll 10 48 39
Output:
Case #0: 3 Case #1: 0
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: The road across Uzbekistan (15 points)
The road is longer now, can you still answer Stofl’s question?
Input & Output
Same as subtask 1.
Limits
There are test cases. For each test case, we have:
- for all
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Interrupting the alarms (10 points)
Stofl doesn’t like merchants being alarmed. Therefore he will hire mercenaries to interrupt the alarms of the merchants. Between any two adjacent merchants, he can hire a mercenary to stop the alarms from spreading further. This will interrupt any alarm signal from passing, not only the alarms from the merchants next to the mercenaries.
The mercenaries are in dire need of money, so they offer their service for mouse coin. In this subtask it holds that .
Input
On the first line on each test case, you will now get two spaced integers and , corresponding to the number of merchants and the price of hiring a mercenary. The rest of the input is the same as subtasks 1 and 2.
Output
For each test case, output a line Case #i: P, where is the minimum amount of money Stofl needs to spend to get all the goods. also includes the amount Stofl spends on mercenaries.
Limits
There are test cases. For each test case, we have:
- for all
Example
Input:
1 4 1 rrll 6 3 5 4
Output:
Case #0: 1
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4: The mercenaries need money (25 points)
The mercenaries between Samarkand and Bukhara do not offer their service for so cheap. Can you still answer’s Stofl question?
Input & Output
Same as subtask 3.
Limits
There are test cases. For each test case, we have:
- for all
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 5: The ultimate heist (40 points)
Stofl wants to rob the entire Silk Road! There are a lot of merchants and the prices can get very high!
Input & Output
Same as subtask 3 and 4.
Limits
There are test cases. For each test case, we have:
- for all
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Emirate of Bukhara
During her travels through time and space Mouse Binna has arrived in the Emirate of Bukhara. In the Chor Minor she has stumbled across a mysterious machine. There is a sequence of boxes in a row, with a sliding cover that always leaves exactly one box uncovered. There seems to be some kind of riddle to be solved from the contests of the boxes. The room Binna is in seems to have a strange effect on her, it messes with her mind and she is very sceptical about her ability to remember anything. Luckily, each of the boxes stores number and additionally Mouse Binna can take some notes. She has reusable notepads available. Each notepad only holds one number at any time, but Mouse Binna can erase and reuse the notepads she does not need anymore. In the beginning there is a on every notepad.
You need to help Mouse Binna solve the problem. Through a space time portal, you can send Mouse Binna instructions on how to operate the machine to solve the problem. To make sure Binna understands your instructions, you need to write it in the following standardised TTL (time travelers language).
Language definition
Your program should be composed of the following operations. You should put one statement per line, statements that take values or condition can be composed of
| Instruction | Explanation |
|---|---|
| MOVE x | Move the head of the machine by to the right if and to the left if |
| READ | Read the value from the current box |
| WRITE v | Write the value into the current box |
| RAMWRITE i v | Write the value into notepad |
| RAMREAD i | Read the value out of the th notepad |
| IF cond | Start an if condition block, if the condition is true, go on to the next line, else jump to END IF |
| END IF | Ends the condition block |
| WHILE cond | Start a while loop. If cond is true, go on to the next line, else jump after the matching END WHILE |
| END WHILE | End of the while loop, jump to the WHILE statement |
| + x y | Compute the sum of x and y |
| * x y | Compute the product of x and y |
| - x y | Compute x - y |
| / x y | Compute x / y, the division is done on integers and rounded towards 0 |
| MOD x y | Compute x mod y, where x mod y is defined as x - (x / y) * y |
| & x y | Compute the bitwise AND of x and y |
| | x y | Compute the bitwise OR of x and y |
| ^ x y | Compute the bitwise XOR of x and y |
| << x y | Compute the value of x shifted to the left by y digits. |
| < x y | Return TRUE if x < y, else return FALSE |
| <= x y | Return TRUE if x <= y, else return FALSE |
| == x y | Return TRUE if x == y, else return FALSE |
| != x y | Return TRUE if x != y, else return FALSE |
| > x y | Return TRUE if x > y, else return FALSE |
| >= x y | Return TRUE if x >= y, else return FALSE |
| ! x | Returns TRUE if x is FALSE and FALSE if x is TRUE |
| && x y | Returns TRUE if x and y are TRUE and FALSE otherwise |
| || x y | Returns FALSE if x and y are FALSE and TRUE otherwise |
| INT cond | Returns 1 if the condition is TRUE and 0 otherwise |
The largest number Mouse Binna knows is . If you try to use numbers that are bigger than that or smaller than Mouse Binna’s brain is gonna explode and your program wraps the number around.
You can use constants in your program by using the standard decimal notation.
Your program can consist of at most lines that execute at most instructions and you can nest at most instructions in one expression.
The head of the machine always starts in the leftmost box.
The sum of over all your move operations can be at most and you have RAM cells to access, i.e., if you call RAMREAD or RAMWRITE with your machine explodes.
Mouse Binna was able to secure a copy of the machine for you so that you can test your code. Download the code as Compile the following code with your favorite C++ compiler (or open and run it in the editor of your choice). Note that the interpreter assumes that there are two files in the same directory: program.txt, the code you want to test and boxes.txt, a file that contains two lines, the first line should contain an integer , the number of boxes. The second line should contain space separated integers, the initial state of the tape.
Subtask 1: Reversing the boxes (7 points)
To start of Mouse Binna want to simply reverse order the values are in.
Input & Limits
The first line contains the number of test cases . test cases follow in the following format:
- The first line contains the integer , the number of Boxes the machine has.
In this subtask will always be 2 and Case 0 will always have and Case 1 will have .
Output
For the -th test case output “Case #i:” followed by your program. Your program should reverse the values in the boxes, i.e., the value of BOX 0 goes into BOX N-1 and the other way round etc.
Evaluation
Your program will be tested on a number of examples. In each example, your program will find a machine with exactly boxes, where each box has a value with .
Scoring
You will get of the points for solving Case 0 and of the points for solving Case 1.
Example
Input:
1 2
Output:
Case #0: RAMWRITE 0 READ MOVE 1 RAMWRITE 1 READ WRITE RAMREAD 0 MOVE -1 WRITE RAMREAD 1
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: Sorting the boxes (15 points)
Now that Binna knows how to reverse the boxes, she wants to approach more difficult tasks. Can you write a program that sorts the number in the boxes in increasing order?
Input & Limits
The first line contains the number of test cases . test cases follow in the following format:
- The first line contains the integer , the number of Boxes the machine has.
In this subtask will always be 3 and Case 0 will always have , Case 1 will have and Case 2 will have .
Output
For the -th test case output “Case #i:” followed by your program. Your program should sort the values in the boxes. I.e. after your program terminates, the smallest value should be in BOX 0, the next smallest in BOX 1, etc.
Evaluation
Your program will be tested on a number of examples. In each example, your program will find a machine with exactly boxes, where each box has a value with .
Scoring
You will get of the points for solving Case 0, of the points for solving Case 1 and of the points for solving Case 2.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Is the graph connected? (18 points)
Mouse Binna remembers that in school she learned about graphs. She wonders if the machine can be used to solve graph theory problems? In the all following subtasks, the input in the boxes are edges of a graph. The vertices of the graph will be labeled . As the boxes are quite small and only fit a single integer, the edge between and is stored as .
You also receive a new instruction to output a boolean answer!
| Instruction | Explanation |
|---|---|
| OUT b | Output a boolean value |
Your program will terminate after the first OUT instruction is reached
Input & Limits
The first line contains the number of test cases . test cases follow in the following format:
- The first line contains two integers and , the number of Boxes the machine has. This number also represents the number of edges in the graph.
In this subtask will always be 4 and Case 0 will always have and , Case 1 will have and , Case 2 will have and , and Case 3 will have and .
Output
For the -th test case output “Case #i:” followed by your program. Your program should output TRUE if the graph described by the edges in the boxes is connected and FALSE otherwise.
Evaluation
Your program will be tested on a number of examples. In each example, your program will find a machine with exactly boxes, where each box has a value with .
Scoring
You will get of the points for solving Case 0, for solving Case 1, of the points for solving Case 2 and of the points for solving Case 3.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4: Is the graph bipartite? (27 points)
Mouse Binna wonders if she can also solve more advanced graph problems. Can you help her figure out whether a graph is bipartite? That means that there is an assignment of the numbers and to the vertices of the graph such that for every edge the two endpoints of the edge have different colors.
You also receive a new instruction to output colors of a vertex!
| Instruction | Explanation |
|---|---|
| COLOUT u c | Output color for vertex |
Your program should again use the OUT istruction from the previous subtask once it determined whether the graph is bipartite. Your program is terminated when you output a bool. After the program terminated, if you outputted OUT TRUE, you should have also outputted a color for every vertex at least once. If you outputted the color of a vertex multiple times, the last color counts. You need to output a correct coloring for all cases where your program returns TRUE.
Input & Limits
The first line contains the number of test cases . test cases follow in the following format:
- The first line contains two integers and , the number of Boxes the machine has. This number also represents the number of edges in the graph.
In this subtask will always be 4 and Case 0 will always have and , Case 1 will have and , Case 2 will have and , and Case 3 will have and .
Output
For the -th test case output “Case #i:” followed by your program. Your program should output TRUE if the graph described by the edges in the boxes is bipartite and FALSE otherwise. If your output was TRUE you should also output a valid coloring of the graph. If the output was FALSE any printed colors will be ignored.
Evaluation
Your program will be tested on a number of examples. In each example, your program will find a machine with exactly boxes, where each box has a value with .
Scoring
You will get of the points for solving Case 0, for solving Case 1, of the points for solving Case 2 and of the points for solving Case 3.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 5: Use as few colors as possible (33 points)
For the final subtask, Mouse Binna finds an arbitrary graph in the machine and wants to color it with as few colors as possible.
Input & Limits
The first line contains the number of test cases . test cases follow in the following format:
- The first line contains two integers and , the number of Boxes the machine has. This number also represents the number of edges in the graph.
In this subtask will always be 4 and Case 0 will always have and , Case 1 will have and , Case 2 will have and , and Case 3 will have and .
Output
For the -th test case output “Case #i:” followed by your program. Your program should use the COLOUT function to output a color for each vertex.
Evaluation
Your program will be tested on a number of examples. In each example, your program will find a machine with exactly boxes, where each box has a value with .
Scoring
You will get of the points for solving Case 0, for solving Case 1, of the points for solving Case 2 and of the points for solving Case 3. Within each subtask, you will be scored against the number of colors that you use.
| Metric | Points |
|---|---|
| better than that | Depending on the number of colors |
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Tomb exploration
Shah-i-Zinda is a famous necropolis (a large old cemetary) in Uzbekistan. Mouse Binna and a large team of passionate archeologists are preparing to enter an old, cursed, and unexplored tomb to bring back all the valuable historical unseen items they can find for the local museum. This project is of the upmost importance as all previous tombs explored were scavenged centuries ago because no curse protected them.
The tomb’s cryptic curse is written in majestic carved letters above the entrance: “He who exits these sacred grounds, shall suffer the weight of his hefty theft.”
Fully prepared to endure the consequences of their actions for the historical sake of the country (the team is as passionate about history as you can get), the entire team led by Binna enters the tomb. They travel multiple galleries with walls covered in beautiful artworks dating back to centuries. They of course progress with great care and take tons of pictures of everything they can see. After hours of exploration – mice have small legs and can’t travel very fast – they finally arrive at the main room of the tomb. On shelves they see small lined up statues which should be brought back to the surface for everyone to enjoy.
In front of this incredible spectacle, Binna can’t resist the urge to keep track of the order of the statues so they can reconstruct the way they are arranged in the museum. She also recalls what the curse said above the entrance and finally understands what it was all about: When exiting the tomb, everyone carrying statues will be inevitably cursed. In addition, for a specific mouse, the curse effect will be proportional to the weight of the heaviest statue they are carrying. The -th statue in the line will have weight . That is, if mouse carries some statues and the heaviest statue is statue with weight , then the curse mouse will suffer will be of importance .
When entering the tomb, the team brought many bags with them, each bag can carry at most statues. Due to the size of the bags relative to the size of a mouse, a mouse can only carry at most bag out of the tomb.
Binna wishes to minimize the sum of the curses the team will have to endure once they leave.
To help them keep track of the order of the many statues, the mice have decided that each bag containing statues will contain statues with incrementing positions. That is, the -th bag containing with statues, will contain the statues at the positions .
The team can use as many bags as they want and there are more than enough mice to carry all the filled bags.
Can you help Binna minimize the sum of the maximum weight of the statues present in each bag?
Input/Output
All subtasks have the same input and output format.
Input
The first line contains the number of test cases . The test cases follow in the following format:
- The first line contains two integers and , the number of statues on shelves and the maximum number of statues a bag can contain respectively.
- The second line contains strictly positive integers. The -th integer is , the weight of the -th statue
Output
For the -th test case, output a line “Case #t:”, followed by the number , the minimum possible sum of the maximum weight of the statues in each bag.
Subtask 1: Ordered statues (17 points)
When inspecting the statues more closely, Binna realizes that the statues weights are monotonic. That is, the statues are sorted from lightest to heaviest or heaviest to lightest.
Limits
- ;
- for all
Example
Input:
2 5 2 7 8 9 10 11 3 3 9 5 2
Output:
Case #0: 27 Case #1: 9
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: Sports bags (18 points)
Binna passed by during her afternoon jogging and only brought some sports bags which can fit 2 statues.
Limits
- ;
- for all
Example
Input:
1 5 2 8 7 10 11 5
Output:
Case #0: 24
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Small bags (24 points)
Binna wasn’t expecting to find so many statues and only brought small bags in the tomb.
Limits
- ;
- for all
Example
Input:
2 5 2 8 7 10 11 5 5 3 1 9 5 4 1
Output:
Case #0: 24 Case #1: 11
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4: The great find (41 points)
The team has never seen as many historical artifacts in one room and have come prepared with large bags.
Limits
- ;
- for all
Example
Input:
2 5 2 8 7 10 11 5 5 3 1 9 5 4 1
Output:
Case #0: 24 Case #1: 11
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Evilruins
Mouse Stofl and Binna are doing multiple cave expeditions in the lands of Uzbekistan, where they try to find crystals and treasures. They already investigated a lot of caves, among which are the famous Boybuloq caverns and the huge Deep Star cave system. In their 33rd expedition, they found something truly terrifying.
At the very bottom of the cave system, they found ruins of an ancient civilization of the “Dark Practitioners”, which was a terrifying cult of moles known for the black magic. In fact, this ruin contains a library full of evil magic that has been lost for centuries. Stofl and Binna need to cover up this ruin as fast as possible such that this dark knowledge doesn’t fall into evil hands.
The cave system is made up of chambers labeled from to . The chambers are all connected to each other through channels. The chamber contains the ruins and is at the very bottom of the cave system. Non ruin chambers with only one channel are cave entrances on the surface, which have different sizes . All other chambers are intermediary and lead down towards the ruins. In order to cover up the ruins, Stofl and Binna have to fill the entire cave system with sand from the nearby Kyzylkum Desert. The red sand of the desert is holy and blocks the dark magic from spreading. They will pour sand into one of the entrances filling up one chamber at a time. The sand will fall down towards the ruins until it reaches them or the next chamber in the direction of the ruins is already filled.
Although both Stofl and Binna want to save the world, they also want to be better than the other one in saving the world. That’s why they take alternating turns pouring sand, starting with Stofl. In one turn, they choose a cave entrance and pour sand into it, filling one chamber or the entrance. If the chamber they fill is the entrance itself, they get points for doing so. They cannot choose an entrance which is already filled and play until there are no unfilled chambers. The mouse with more points in the end is deemed “Hero of the world”.
Given the map of the caves, you will need to determine who will get more points by filling up entrances.
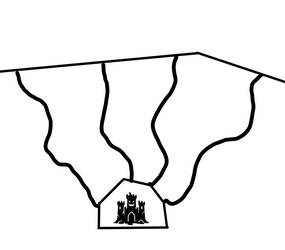
Subtask 1: Direct channels (6 points)
Every entrance leads directly to the ruins, with no chambers in between.
An example of a valid structure would look like this:
Input
The first line contains the number of test cases . For each test case, you will get following lines:
- The first line contains , denoting the number of chambers.
- The second line contains integers , denoting the number of points per chamber. Note that it will be for chambers not on the surface.
- The next lines contains two integers which denotes a channel between chamber and .
Output
For each test case, output a single line Case #i: P where where is the points Stofl gets and the points Binna gets, assuming they fill up the cave system optimally.
Limits
- for all
Example
Input:
2 4 0 3 2 5 2 0 0 1 3 0 5 0 1 1 1 1 3 0 0 1 0 4 2 0
Output:
Case #0: -4 Case #1: 0
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
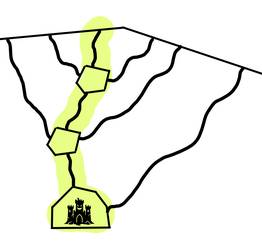
Subtask 2: Transportation channels (10 points)
The channels have been dug in a very specific way. There is a central chamber line, and each chamber on that line has zero or more channels directly leading to a cave entrance. They probably used it as a logistics cave.
An example of a valid structure would look like this, where the yellow line indicates central chamber line.
Input, Output & Limits
Same as in subtask 1.
Example
Input:
2 3 0 0 3 1 2 1 0 9 0 0 0 4 3 2 5 7 2 4 1 2 8 1 5 3 0 1 0 6 2 7 2 1 2
Output:
Case #0: 3 Case #1: -1
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Guard chambers (19 points)
Stofl and Binna noticed something interesting: The intermediary chambers have channels only directly to the ruins or entrances. They were likely used as guard post, providing a direct path to the city, but blocking off unwanted visitors from the surface. In addition, a direct path between an entrance at the surface and the ruins never exists.
An example of a valid structure would look like this:
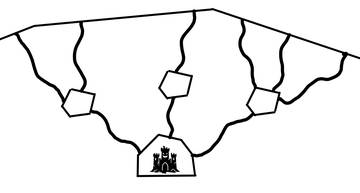
Input, Output & Limits
Same as in subtask 1 and 2.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Example
Input:
2 4 0 0 2 9 1 0 1 2 3 1 10 0 0 0 0 4 2 2 6 2 9 0 3 3 9 0 1 8 3 1 4 5 1 2 0 6 2 3 7
Output:
Case #0: 7 Case #1: -5
Subtask 4: Collapsed chambers (8 points)
Binna and Stofl are now interested in general cave systems. For now, they are only concerned in systems where many chambers have collapsed under the rocks. So, not many chambers are accessible anymore.
Input & Output
Same as previous subtasks
Limits
- for all
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 5: Equally sized entrances (14 points)
Stofl and Binna have big ambitions and want to also solve large general cave systems. Luckily, for now, the entrances look exactly the same, thus covering them up gives the same amount of points. They feel otherworldly…
Input & Output
Same as previous subtasks
Limits
- For all chambers on the surface .
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 6: The evil aura (43 points)
The evil aura surrounding the ruins created a very spooky and huge cave system. This feels like the work of a divine being, which was able to hold this huge alien cave system together after all the years.
This is the final test, who is the true hero of the world?
Input & Output
Same as previous subtasks
Limits
- for all
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
2H
The homework part of the second round (2H) consists of 4 tasks, each of which is worth 25 points. You can gain a maximum of 100 points counting towards your score of the regular round.
2H GraderThis helps you get familiar with our grading system which we will use in all our events after the second round, including workshops, camp, finals, and team selection.
You can submit in C++ (recommended), Java or Python.
| C++: | If you don’t have a setup already, we recommend installing VSCode. |
|---|---|
| Java: | Read Java on the SOI Grader. |
| Python: | Read Python on the SOI Grader. |
For 2H you can discuss solutions with friends or publicly on Discord, as long as you don’t share source code. We are also happy to help you! If you need help with the grading system or have questions regarding the theory or tasks, don’t hesitate to ask here or in Discord.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Junior Ranking
| Rank | Username | Total (600) | regista… (100) registanpattern | timurid… (100) timuridriders | mouseda… (100) mousedances | fire (100) | roborbuy (100) | bukhara (100) |
|---|---|---|---|---|---|---|---|---|
| loading ... |
Regular Ranking
| Rank | Username | Total (700) | mouseda… (100) mousedances | fire (100) | roborbuy (100) | bukhara (100) | tombexp… (100) tombexploration | evilruins (100) | 2h (100) |
|---|---|---|---|---|---|---|---|---|---|
| loading ... |
In the first testcase, the first rider will start at village 1, then go to village 0. The next rider starts at village 2, but the next village, 0, is already occupied, so they stay at village 2.
In the second testcase, the first rider will start at village 2, then go to village 1, then go to village 0.