Written by Daniel Wolleb-Graf and Raphael Fischer.
Dieses Kapitel geht davon aus, dass du bereits weisst was ein Graph ist und wie wir ihn als Adjazenzliste darstellen können. Lies also unbedingt zuerst das Kapitel Graphentheorie - zumindest den Anfang - falls dir das noch nicht bekannt vorkommt.
Standardalgorithmus
Was steckt hinter der oft gebrauchten Abkürzung DFS?
Nun wollen wir uns an den ersten Algorithmus für Graphen heranwagen. Es ist die sogenannte Tiefensuche, oft abgekürzt mit DFS, vom Englischen Depth First Search. Sie ist eine von zwei sogenannten Graphentraversierungsalgorithmen, die in den Rucksack eines jeden Informatik-Olympioniken gehören. Den anderen, die Breitensuche (BFS), schauen wir gleich nachher an. Bei beiden geht es darum, den Graphen systematisch zu erkunden und zu entdecken oder eben zu traversieren.
Stell dir vor du steckst mitten in einem Labyrinth. Das Labyrinth beschreiben wir als Graphen mit den Räumen als Knoten und den Gängen zwischen den Räumen als Kanten. Wir stecken nun völlig verloren im Raum/Knoten Nr. 0 und suchen den Ausgang (sei dies Knoten n-1). Alle Räume sehen etwa gleich aus und wir haben keinen Lageplan, kein GPS, kein Wifi und auch sonst kaum Hilfsmittel. Alles was wir haben ist ein langer roter Faden und ein grosser Topf mit roter Farbe.
Wie finden wir nun den Ausgang aus dem Labyrinth?
Unsere Strategie ist die folgende: Wir fixieren den Faden, den wir nachher während unserem Erkundungsgang abrollen werden, in unserem Startraum, sodass wir den Weg zurück zu diesem Startraum stets wieder finden können. Ausserdem malen wir einen roten Punkt auf den Boden, um zu markieren, dass wir den Startraum schon besucht haben.
Wir starten in eine beliebige Richtung und machen in jedem neuen Raum folgendes: Wir malen einen roten Punkt auf den Boden, damit wir wissen, dass wir hier schon waren, und klappern dann der Reihe nach von links nach rechts alle ausgehenden Gänge ab. Das heisst wir gehen zuerst dem linkesten Gang entlang und kommen so wieder in einen neuen Raum. Dort bringen wir eine Markierung an und gehen wieder dem linkesten Gang nach weiter. Irgendwann kommen wir so in eine Sackgasse oder in einen Raum, in dem wir schon einmal waren (der also schon eine rote Markierung auf dem Boden hat). In einem solchen Fall kehren wir einfach um und gehen zurück zum Raum, aus dem wir gekommen sind (der rote Faden sagt uns, wo das war). Von dort probieren wir es mit dem nächsten Gang, den es noch zu erkunden gilt (den nächsten von links) und wiederholen das gleiche Verfahren. So probieren wir systematisch Gang für Gang durch. Haben wir auch den letzten, rechtesten Gang erkundet, so beenden wir die Suche in diesem Raum und gehen einen Gang zurück in Richtung Startraum (indem wir dem roten Faden folgen). Auf diese Weise finden wir früher oder später den Ausgang oder wissen, dass er vom Start aus unerreichbar ist.
Algorithmus: Tiefensuche
Genau so funktioniert nun auch die Tiefensuche. Den Farbtopf simulieren wir mit einem booleschen Array, also einem Bit pro Raum, mit dem wir uns merken, ob wir einen bestimmten Raum schon besucht haben oder nicht. Den Faden repräsentieren wir nur implizit, nämlich mit dem rekursiven Aufruf-Stack unserer DFS-Funktion. Das heisst in jedem Aufruf der DFS-Funktion besuchen wir einen neuen Knoten und rufen die Funktion rekursiv für alle von dort benachbarten, noch nicht besuchten Knoten auf. Hier sieht du eine mögliche Implementation in C++ und in Python:
Beispiel
Schauen wir uns das an einem kleinen Beispiel an. Im Graph unten sind die Knoten in der Reihenfolge nummeriert, in welcher sie von der Tiefensuche besucht werden. Die Pfeilrichtungen zeigen an, von wo aus der jeweilige Knoten entdeckt wird. So wird der 7. Knoten beispielsweise vom 3. Knoten aus entdeckt. Später wird dieser Knoten vom 1. Knoten aus nochmals betrachtet, dann aber ignoriert, da dann sein visited Eintrag bereits auf true gesetzt wurde.
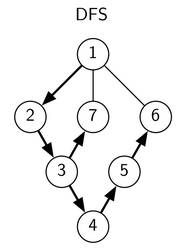
Bild 1: Beispielgraph mit den Knoten nummeriert in der Reihenfolge, in welcher sie von einer Tiefensuche entdeckt werden.
Um diesen Beispielgraphen in das obige Programm einzugeben, könnte man zum Beispiel folgendes eingeben (beachte, dass die Knoten für unseren Code nullbasiert nummeriert werden müssen):
7 8 0 1 1 2 0 6 0 5 2 6 4 5 2 3 3 4
Anwendungen: Und wozu ist das gut?
Zusammenhangskomponenten bestimmen
Eine solche Tiefensuche kann uns also beantworten, ob zwei Knoten direkt oder indirekt verbunden sind oder nicht. Die Menge aller Knoten, die gegenseitig miteinander verbunden sind, nennt man auch Zusammenhangskomponente. Der Graph in Bild 2 besteht aus zwei solchen Zusammenhangskomponenten. Die Knoten 1 bis 4 bilden die eine, die Knoten 5 und 6 die andere Komponente. Um alle Zusammenhangskomponenten mittels Tiefensuche zu bestimmen, gehen wir einmal durch alle Knoten und starten bei jedem noch unbesuchten Knoten eine Tiefensuche. Jedes Mal wenn wir eine neue Tiefensuche starten, entdecken wir eine neue Komponente.
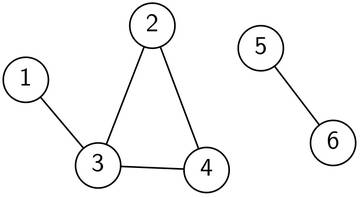
Bild 2: Ein Beispiel für einen Graphen mit 6 Knoten und 5 Kanten.
Zweifärben
Eine weitere nützliche Anwendung ist das Zweifärben von Graphen. Wir möchten dabei jeden Knoten eines Graphen entweder rot oder blau einfärben, sodass keine zwei benachbarten Knoten dieselbe Farbe bekommen. Ist das immer möglich? Nein. In einem Dreieck geht das beispielsweise nicht. Wenn du dir das ein wenig genauer überlegst, siehst du, dass eine gültige Zweifärbung genau dann möglich ist, wenn der Graph keinen Zyklus ungerader Länge enthält, es also keinen Weg gibt, der nach einer ungeraden Anzahl Schritte wieder bei seinem Startpunkt angelangt.
Der Graph in Bild 2 ist nicht zweifärbbar, da das Dreieck 2-3-4 eine Zweifärbung verunmöglicht. Bild 3 zeigt dir einen zweifärbbaren Graphen.
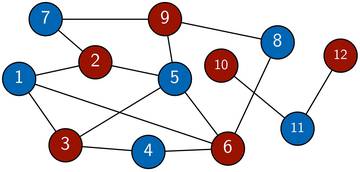
Bild 3: Ein Beispiel eines zweifärbbaren Graphen, der aus zwei Zusammenhangskomponenten besteht.
Eine Art eine solche Färbung zu finden (oder herauszufinden, dass es gar keine solche gibt) ist mittels Tiefensuche. Wenn wir den Startknoten rot markieren, dann müssen alle seine Nachbarn blau sein und alle deren Nachbarn wieder rot und so weiter. Sobald wir also die Farbe des Startknotens wählen, ist die Färbung für die gesamte Zusammenhangskomponente fixiert. Die Tiefensuche erlaubt uns nun diese Färbung zu simulieren und gleichzeitig zu überprüfen, ob es irgendwo zu einem Konflikt kommt, also zu zwei gleichgefärbten, benachbarten Knoten. In der Implementierung ersetzen wir dazu einfach “visited” durch “color”, wobei wir 0 für ungefärbt, 1 für rot und 2 für blau stehen lassen. Innerhalb der DFS-Schleife prüfen wir dann:
Finden eines Zyklus
Eine weitere Aufgabe, die man mit DFS lösen kann, ist herauszufinden, ob ein Graph einen Zyklus enthält. Ein solcher existiert, falls die DFS einen schon besuchten Knoten “neu entdeckt”, also der Knoten, der aktuell das Argument der rekursiven Funktion ist, einen Nachbar hat, den die DFS schon zuvor markiert hatte. Grafisch veranschaulicht sieht das dann so aus:
Nehmen wir an, die Tiefensuche hat bei begonnen und ist dem roten Pfad gefolgt (der sogenannte DFS-Tree), zuerst in Richtung e, nun sei sie bei . Von aus wird nun unter anderem der Nachbar geprüft, der schon zuvor besucht worden war. Somit wurde ein Zyklus gefunden, denn von nach gibt es zwei verschiedene Pfade: Einmal direkt und einmal über den Weg, den die Tiefensuche zuvor genommen hat.
Nun gibt es jedoch noch ein kleines “Problem”: Die Tiefensuche überprüft in jedem Schritt automatisch einen schon besuchten Knoten, und zwar den, von dem die DFS-Funktion aufgerufen wurde. Via diesen Knoten gibt es natürlich keinen Zyklus. Um dieses Problem zu beheben, führen wir ein zweites Argument für unsere DFS-Funktion ein: Der “Parent-Knoten”, also der, von dem aus die Funktion aufgerufen wurde:
Ausblick
Im nächsten Kapitel lernst du die eng mit der Tiefensuche verwandte Breitensuche kennen, mit der sich auch kürzeste Wege bestimmen lassen. Es gibt aber auch noch viele weitere Anwendungen für die Tiefensuche. Eine davon folgt im Kapitel zur “topologischen Sortierung” und in späteren SOI-Runden wirst du auch noch den Algorithmen zur Bestimmung von Artikulationspunkten und Brücken begegnen, welche ebenfalls auf der Tiefensuche aufbauen.
Tasks
We recommend to solve the following tasks.
- dfs:
You need to log in in order to submit for this task.
This is the 2H task about DFS