Tiefensuche
Diese und die nächsten paar Aufgaben handeln von der sogenannten Graphentheorie. Wenn du das Wort “Graphentheorie” nun gerade zum ersten Mal hörst/liest, sagt dir das vermutlich nicht viel. “Graphein” ist griechisch für “schreiben”, was auch nicht viel aussagt. Mit dem Zeichnen zweidimensionaler Funktionsgraphen, das du vielleicht aus dem Mathematikunterricht kennst, hat es auch nichts zu tun. Und “Theorie” soll hier nicht heissen, dass es sich um ungetestete Behauptungen handelt, sondern vielmehr um allgemeine Konzepte, die in sehr vielen Situationen anwendbar sind.
Problembeschreibung
Was ist ein Graph?
Als Graphen bezeichnen wir eine Menge von Punkten und Verbindungen zwischen diesen Punkten. Die Punkte werden meist Knoten und die Verbindungen zwischen Punktepaaren meist Kanten genannt. Im Bild 1 siehst du ein Beispiel eines solchen Graphen. Jeder Kreis ist ein Knoten und jede Linie, die zwei solche Knoten verbindet, ist also eine Kante.
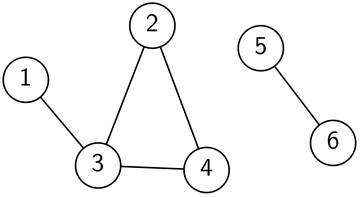
Bild 1: Ein Beispiel für einen Graphen mit 6 Knoten und 5 Kanten.
Dieser Graph besteht also aus 6 Knoten und 5 Kanten. Eine der fünf Kanten verläuft zwischen Knoten und , daher sagen wir, dass Knoten mit Knoten benachbart ist. Die beiden Knoten sind auch indirekt benachbart, nämlich über den gemeinsamen Nachbarn . Häufig sprechen wir von der Nachbarschaft eines Knotens, was einfach die Menge aller Nachbarn bezeichnet. Die Nachbarschaft von sind die Knoten , und und die Nachbarschaft von sind die Knoten und .
Einen Graphen so aufzuzeichnen ist eine Art ihn darzustellen. Auf die genaue Zeichnungsart kommt es uns aber gar nicht an. Wenn wir die Knoten ein wenig verschieben und die Kanten entsprechend mitbewegen, sagen wir immer noch, dass dies derselbe Graph ist. Es muss auch gar nicht unbedingt eine solche Zeichnung sein, wir können einen Graphen auch einfach als abstrakte Liste von Knoten und Kanten beschreiben. Dazu benennen wir oft die Knotenmenge mit (Englisch vertices) und die Kantenmenge mit (Englisch edges). Das Beispiel im Bild 1 wäre dann und . Die Anzahl Knoten bezeichnen wir meist mit (im Beispiel ist ) und die Anzahl Kanten mit (im Beispiel ist ).
Wie sieht ein Graph im Computer aus?
Wenn wir nun in einer Aufgabe der SOI einem solchen Graphen begegnen, so ist dieser meist nicht als Bild gegeben, sondern als solch eine abstrakte Auflistung der Knoten und Kanten. Die Knoten sind dann meist einfach von bis nummeriert und so enthält die Eingabe nur eine Zeile mit und und dann Zeilen mit den Punktepaaren der Kanten. Etwa so (für das Beispiel in Bild 1):
6 5 1 3 2 3 2 4 3 4 5 6
Und was machen wir jetzt damit? Wie repräsentieren wir diesen Graphen nun in unserem Programm, sodass wir nützliche Dinge damit anstellen können? Wir könnten einfach diese Kantenliste so einlesen und abspeichern. In C++ sähe das vielleicht etwa so aus:
int n = 6; int m = 5; vector<pair<int,int>> E = {{1,3}, {2,3}, {2,4}, {3,4}, {5,6}};
Eine solche Kantenliste ist manchmal gut genug und kann alles was wir brauchen. Häufig aber wollen wir auf den Nachbarschaften von Knoten operieren, d.h. wir wollen alle Nachbarn eines Knotens abfragen, was mit einer Kantenliste nur möglich ist, indem wir alle Kanten durchgehen und schauen ob irgendwo vorkommt.
SOI-typische Graphenaufgaben haben oft bis zu Kanten, und da kann eine solche lineare Suche durch die Kantenliste schon mal etwas länger dauern. Deshalb ist die nützlichste Speicherart für Graphen eine andere, nämlich die sogenannte Adjazenzliste. Die Idee ist simpel: Statt einer grossen langen Liste mit allen Kanten merken wir uns für jeden Knoten eine separate Liste mit all seinen Nachbarn. Die Datenstruktur besteht also aus Listen, und wenn wir die Nachbarschaft des Knotens wissen wollen, schauen wir einfach die -te dieser Listen an.
Implementieren lässt sich das in C++ ganz leicht mittels Vektoren, den Arrays dynamischer Grösse (hat nicht viel mit den Vektoren aus der Mathe zu tun). Wir verschachteln dazu Vektoren in einen grossen Vektor - die inneren Vektoren sind die Nachbarschaftslisten und der äussere Vektor hält sie alle zusammen. Ein wenig müssen wir noch wegen der nullbasierten Indexierung aufpassen: entweder wir wandeln alles in nullbasierte Indexierung um (was häufig einfacher geht), oder wir fügen einfach noch einen imaginären Knoten ohne Nachbarn hinzu:
int n = 6; int m = 5; // Erste Variante mit nullbasierte Knoten (von 0 bis n-1 nummeriert): vector<vector<int>> E = {{2}, {2,3}, {0,2,3}, {1,2}, {5}, {4}}; // oder mit einem 0-ten Knoten ohne Nachbarn: vector<vector<int>> E = {{}, {3}, {3,4}, {1,3,4}, {2,3}, {6}, {5}}; // Die Nachbarn von Knoten x sind dann in E[x] zu finden.
Was stellt ein Graph dar?
Ein solcher Graph kann nun für alles mögliche stehen - zum Beispiel für den Strassenplan einer Stadt. Die Knoten stehen dann für die Kreuzungen und Plätze der Stadt und die Kanten für die Strassen dazwischen. Was wir häufig wissen wollen ist zum Beispiel der kürzeste Weg zwischen zwei Knoten (Wie komme ich am schnellsten zum Bahnhof?) oder ob es überhaupt möglich ist, von jedem Ort an jeden anderen zu kommen (Gibt es eine Insel von der man nicht mehr wegkommt?).
Manchmal sind dafür noch Zusatzinformationen zu den Knoten und Kanten gegeben, zum Beispiel eine Fahrtzeit pro Kante (ein sogenanntes Kantengewicht) oder eine Richtung pro Kante (z.B. für Einbahnstrassen). In diesem Kapitel schauen wir uns aber vorerst nur mal ungewichtete, ungerichtete Graphen an.
Standardalgorithmus
Was ist nun diese ominöse DFS?
Nun wollen wir uns an den ersten Algorithmus für Graphen heranwagen. Es ist die sogenannte Tiefensuche, oft abgekürzt mit DFS, vom Englischen Depth First Search. Sie ist eine von zwei sogenannten Graphentraversierungsalgorithmen, die in den Rucksack eines jeden Informatik-Olympioniken gehören. Den anderen, die Breitensuche (BFS), schauen wir gleich nachher an. Bei beiden geht es darum, den Graphen systematisch zu erkunden und zu entdecken oder eben zu traversieren.
Stell dir vor du steckst mitten in einem Labyrinth. Das Labyrinth beschreiben wir als Graphen mit den Räumen als Knoten und den Gängen zwischen den Räumen als Kanten. Wir stecken nun völlig verloren im Raum/Knoten Nr. und suchen den Ausgang (sei dies Knoten ). Alle Räume sehen etwa gleich aus und wir haben keinen Lageplan, kein GPS, kein Wifi und auch sonst kaum Hilfsmittel. Alles was wir haben ist ein langer roter Faden und ein grosser Topf mit roter Farbe.
Wie finden wir nun den Ausgang aus dem Labyrinth? Unsere Strategie ist die folgende: Wir fixieren den Faden, den wir nachher während unserem Erkundungsgang abrollen werden, in unserem Startraum, sodass wir den Weg zurück zu diesem Startraum stets wieder finden können. Ausserdem malen wir einen roten Punkt auf den Boden, um zu markieren, dass wir den Startraum schon besucht haben. Wir starten in eine beliebige Richtung und machen in jedem neuen Raum folgendes: Wir malen einen roten Punkt auf den Boden, damit wir wissen, dass wir hier schon waren und klappern dann der Reihe nach von links nach rechts alle ausgehenden Gänge ab. Das heisst wir gehen zuerst dem linkesten Gang entlang und kommen so wieder in einen neuen Raum. Dort bringen wir eine Markierung an und gehen wieder dem linkesten Gang nach weiter. Irgendwann kommen wir so in eine Sackgasse oder in einen Raum in dem wir schon einmal waren (der also schon eine rote Markierung auf dem Boden hat). In einem solchen Fall kehren wir einfach um und gehen zurück zum Raum aus dem wir gekommen sind (der rote Faden sagt uns wo das war). Von dort probieren wir es mit dem nächsten Gang, den es noch zu erkunden gilt (den nächsten von links) und wiederholen das gleiche Verfahren. So probieren wir systematisch Gang für Gang durch. Haben wir auch den letzten, rechtesten Gang erkundet, so beenden wir die Suche in diesem Raum und gehen einen Gang zurück in Richtung Startraum (indem wir dem roten Faden folgen). Auf diese Weise finden wir früher oder später den Ausgang oder wissen, dass er vom Start aus unerreichbar ist.
Algorithmus: Tiefensuche
Genau so funktioniert nun auch die Tiefensuche. Den Farbtopf simulieren wir mit einem booleschen Array, also einem Bit pro Raum, mit dem wir uns merken, ob wir einen bestimmten Raum schon besucht haben oder nicht. Den Faden repräsentieren wir nur implizit, nämlich mit dem rekursiven Aufruf-Stack unserer DFS-Funktion. Das heisst in jedem Aufruf der DFS-Funktion besuchen wir einen neuen Knoten und rufen die Funktion rekursiv für alle von dort benachbarten, noch nicht besuchten Knoten auf. In C++ Code sieht das dann etwa so aus:
// Wir nehmen an, dass E eine nullbasierte Adjazenzliste darstellt. vector<vector<int>> E; vector<int> visited; void dfs(int v) { // Wir sind in Knoten v und erkunden die Nachbarschaft. for(int e = 0; e < E[v].size(); e++) { int w = E[v][e]; // Nun prüfen wir ob der Nachbar w noch unbesucht ist. if(!visited[w]) { visited[w] = true; dfs(w); } } } int main() { // Wir beginnen damit E einzulesen, z.B. so: int n, m; cin >> n >> m; E = vector<vector<int>>(n); for(int i = 0; i < m; i++) { int a, b; cin >> a >> b; E[a].push_back(b); E[b].push_back(a); } // Nun können wir unsere Tiefensuche starten int start = 0; visited = vector<int>(n, false); // Zu Beginn haben wir noch nichts besucht. visited[start] = true; dfs(start); // Ob der Ausgang erreicht werden kann, können wir nun ganz leicht ablesen. cout << "Kann der Ausgang erreicht werden?\n"; if(visited[n-1]) { cout << "Ja!\n"; } else { cout << "Nein!\n"; } }
Und wozu ist das gut?
Eine solche Tiefensuche kann uns also beantworten, ob zwei Knoten direkt oder indirekt verbunden sind oder nicht. Die Menge aller Knoten, die gegenseitig miteinander verbunden sind, nennt man auch Zusammenhangskomponente. Der Graph in Bild 1 besteht aus zwei solchen Zusammenhangskomponenten. Die Knoten bis bilden die eine, die Knoten und die andere Komponente. Um alle Zusammenhangskomponenten mittels Tiefensuche zu bestimmen, gehen wir einmal durch alle Knoten und starten bei jedem noch unbesuchten Knoten eine Tiefensuche. Jedesmal wenn wir eine neue Tiefensuche starten, entdecken wir eine neue Komponente.
Eine weitere nützliche Anwendung ist das Zweifärben von Graphen. Wir möchten dabei jeden Knoten eines Graphen entweder rot oder blau einfärben, sodass keine zwei benachbarten Knoten dieselbe Farbe bekommen. Ist das immer möglich? Nein. In einem Dreieck geht das beispielsweise nicht. Wenn du dir das ein wenig genauer überlegst, siehst du, dass eine gültige Zweifärbung genau dann möglich ist, wenn der Graph keinen Zyklus ungerader Länge enthält, es also keinen Weg gibt, der nach einer ungeraden Anzahl Schritte wieder bei seinem Startpunkt angelangt.
Der Graph in Bild 1 ist nicht zweifärbbar, da das Dreieck eine Zweifärbung verunmöglicht. Bild 2 zeigt dir einen zweifärbbaren Graphen.
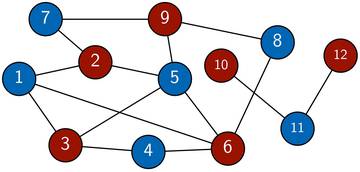
Bild 2: Ein Beispiel eines zweifärbbaren Graphen, der aus zwei Zusammenhangskomponenten besteht.
Eine Art eine solche Färbung zu finden (oder herauszufinden, dass es gar keine solche gibt) ist mittels Tiefensuche. Wenn wir den Startknoten rot markieren, dann müssen alle seine Nachbarn blau sein und alle deren Nachbarn wieder rot und so weiter. Sobald wir also die Farbe des Startknotens wählen, ist die Färbung für die gesamte Zusammenhangskomponente fixiert. Die Tiefensuche erlaubt uns nun diese Färbung zu simulieren und gleichzeitig zu überprüfen, ob es irgendwo zu einem Konflikt kommt, also zu zwei gleichgefärbten, benachbarten Knoten. In der Implementierung ersetzen wir dazu einfach “visited” durch “color”, wobei wir 0 für ungefärbt, 1 für rot und 2 für blau stehen lassen. Innerhalb der DFS-Schleife prüfen wir dann:
bool dfs(int v) { // Wir sind in Knoten v und erkunden die Nachbarschaft. for(int e = 0; e < E[v].size(); e++) { int w = E[v][e]; // Nun prüfen wir ob der Nachbar w noch unbesucht ist. if(color[w]==0) { // Setze w auf die andere Farbe als v. color[w] = 3-color[v]; // Rekursiere und brich ab, sobald ein Fehler gefunden wurde: if(!dfs(w)) { return false; } } else { // Prüfe, dass v und w unterschiedliche Farbe haben. if(color[v] == color[w]) { // Der Graph ist in diesem Fall nicht zweifärbbar, was wir beispielsweise mit dem Rückgabewert mitteilen können. return false; } } } return true; }
Aufgabe
Gegeben ein ungerichteter, ungewichteter Graph, entscheide ob es möglich ist, seine Knoten mit zwei Farben zu färben, sodass keine zwei benachbarten Knoten die selbe Farbe erhalten.
Eingabe
Auf der ersten Zeile steht die Zahl , die Anzahl Testfälle. Es folgen Graphenbeschreibungen mit jeweils dem folgenden Format: Auf der ersten Zeile steht und , die Anzahl Knoten und Kanten. Anschliessend folgen Zeilen, welche die Kanten mittels je zweier nullbasierter Indices beschreiben. Eine Zeile mit und bedeutet, dass der Knoten mit Knoten verbunden ist (und umgekehrt). Beachte, dass die Knoten nullbasiert indexiert sind. Sie sind also von bis nummeriert.
Ausgabe
Gib für den -ten Testfall “Case #t:” aus, gefolgt von “YES” oder “NO”, je nachdem ob der -te Graph zweifärbbar ist oder nicht.
Limits
Beispiele
Input:
1 6 5 0 2 1 2 1 3 2 3 4 5
Output:
Case #1: NO
Comment:
Input:
1 7 6 0 1 2 1 5 3 4 3 4 6 5 6
Output:
Case #1: YES
Comment:
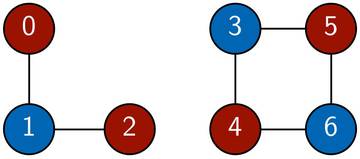
Bild 3: Der zweifärbbare Graph des zweiten Beispiels.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Anmerkung: Eine Anwendung dieses Zweifärbeproblems war die erste Hälfte der Aufgabe “River” der ersten Runde der SOI 2015. Du kannst die Aufgabe hier nachlesen und du findest hier die Lösungsbeschreibung.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Breitensuche
Der Unterschied zwischen der Tiefensuche, welche wir im vorhergehenden Tutorial kennengelernt haben, und der Breitensuche, die wir jetzt anschauen werden, ist ein kleiner aber feiner. Abgekürzt wir die Breitensuche oft einfach mit BFS (für das Englische breadth first search).
Problembeschreibung
Wie wir gesehen haben, erlaubt uns die Tiefensuche die Zusammenhangskomponenten eines Graphen zu bestimmen oder ihn mit zwei Farben zu färben. Was wir aber bisher noch nicht können, ist das Finden von kürzesten Wegen zwischen zwei Knoten. Die Breitensuche wird uns dies ermöglichen.
Standardalgorithmus
Breitensuche - Woher kommt der Name?
In der Tiefensuche stürzten wir uns Hals über Kopf in die Tiefe des Graphen. Wir schlugen einfach mal eine willkürliche Richtung ein und gingen so lange weiter bis wir umkehren mussten, weil wir nichts Neues mehr entdecken konnten. Erst dann schauten wir uns nach möglichen alternativen Abzweigungen um.
Die Breitensuche geht nun - wie der Name suggeriert - zuerst in die Breite statt in die Tiefe. Wir wollen zuerst alles erkunden, was unmittelbar zum Startpunkt benachbart ist. Erst danach schauen wir uns Knoten mit Distanz an, also die Nachbarn der Nachbarn. Und erst wenn wir alle diese Nachbarn zweiten Grades besucht haben, dann erst beginnen wir mit den Nachbarn der Nachbarn der Nachbarn. Und so weiter.
Algorithmus: Breitensuche
Diese Idee lässt sich am einfachsten mit Hilfe einer Warteschlange (Englisch queue) implementieren. Darin merken wir uns alle Knoten, die wir entdeckt haben, deren Nachbarn wir uns aber noch anschauen wollen.
Bei der Tiefensuche erfolgten diese zwei Schritte jeweils unmittelbar hintereinander, also sobald wir einen Knoten entdeckt haben, haben wir auch gleich damit begonnen seine Nachbarn anzuschauen. Das hat uns erlaubt, die Tiefensuche mittels Rekursion zu implementieren. Nun wollen wir aber für die Breitensuche, dass wir zuerst alle Nachbarn ersten Grades anschauen, bevor wir den ersten Nachbarn zweiten Grades anschauen. Die Warteschlange simuliert nun dieses “Hinten-Anstellen-und-Warten” der neu entdeckten Knoten. In C++ kann das dann etwa so aussehen:
// Wir nehmen wieder an, dass E eine nullbasierte Adjazenzliste darstellt. vector<vector<int>> E; vector<int> visited; void bfs(int start) { queue<int> Q; // Die Warteschlange für die neu entdeckten Knoten. Q.insert(start); while(!Q.empty()) { int v = Q.front(); Q.pop(); // Wir sind in Knoten v und erkunden die Nachbarschaft. for(int e = 0; e < E[v].size(); e++) { int w = E[v][e]; // Nun prüfen wir, ob der Nachbar w noch unbesucht ist. if(!visited[w]) { visited[w] = true; // Anstelle des rekursiven Aufruf der DFS, // fügen wir w nun lediglich in die Schlange ein. Q.insert(w); } } } } int main() { // Graph einlesen, wie zuvor. ... // Nun können wir die Breitensuche starten int start = 0; visited = vector<int>(n, false); // Zu Beginn haben wir noch nichts besucht. visited[start] = true; bfs(start); // In visited[] können wir nun wiederum ablesen, ob // ein bestimmter Knoten erreicht werden kann. }
Bild 1 zeigt dir an einem Beispiel wie sich die Besuchsreihenfolge der Knoten in einer Breitensuche und einer Tiefensuche unterscheiden können.
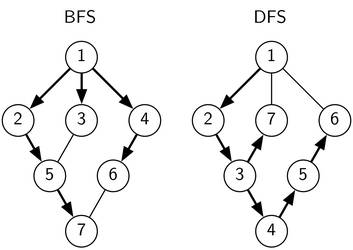
Bild 1: Die Breitensuche (links) und Tiefensuche (rechts) auf dem selben Graphen. Die Zahlen geben die Entdeckungsreihenfolge der Knoten an und die Pfeile bezeichnen die Kanten entlang welcher die Knoten entdeckt wurden.
Kürzeste Wege
Für ungerichtete, ungewichtete Graphen erlaubt uns die Breitensuche die Länge des kürzesten Weges zwischen dem Startpunkt und jedem beliebigen anderen Knoten zu bestimmen. Die Länge eines Pfades messen wir in der Anzahl Kanten, denen wir entlanggehen. Ungewichtet heisst hier also, dass jede Kante als gleich lang gezählt wird. Falls die Kanten unterschiedliche Länge haben, genügt die Breitensuche nicht mehr, um den kürzesten Weg zu berechnen. Der Algorithmus von Dijkstra, welcher dir in einer anderen Aufgabe erklärt wird, löst aber genau dieses Problem. Aber wie berechnen wir nun die ungewichtete Länge des kürzesten Weges von nach mit Hilfe der Breitensuche?
Die Erkundungsreihenfolge der BFS hat die schöne Eigenschaft, dass wir die Knoten in aufsteigender Distanz zum Startknoten besuchen. Das heisst, alle Knoten mit Distanz besuchen wir unmittelbar nach den Knoten mit Distanz und umittelbar vor den Knoten mit Distanz . Wenn immer wir also einen neuen Knoten entdecken, können wir dessen Distanz zum Start direkt bestimmen, nämlich als die Distanz zum aktuellen Knoten plus .
In der Implementierung von oben können wir dies einbauen, indem wir zum Beispiel einen Vektor dist hinzufügen, den wir für jeden Knoten mit unendlich initialisieren (oder einfach einer fixen, sehr grossen Zahl) und dann dist[start] auf Null setzen. Die Distanz der neu entdeckten Knoten setzen wir dann hier mit einer einzigen neuen Zeile:
... if(!visited[w]) { visited[w] = true; // Anstelle des rekursiven Aufruf der DFS, // fügen wir w nun lediglich in die Schlange ein. Q.insert(w); dist[w] = dist[v] + 1; // Neue Zeile! } ...
Bild 2 zeigt nochmals denselben Graphen aber jetzt mit den Distanzangaben zwischen den Knoten und dem Start.
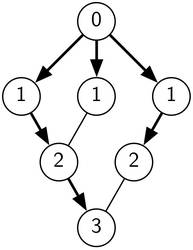
Bild 2: Die Distanzen nach einer Breitensuche, die beim obersten Knoten begonnen hat.
Aufgabe
Du sollst nun diese Breitensuche implementieren, um die Distanz zwischen dem ersten und letzten Knoten eines Graphens zu bestimmen.
Eingabe
Auf der ersten Zeile steht die Zahl , die Anzahl Testfälle. Es folgen Graphenbeschreibungen mit jeweils dem folgenden Format: Auf der ersten Zeile steht und , die Anzahl Knoten und Kanten. Anschliessend folgen Zeilen, welche die Kanten mittels je zweier nullbasierter Indices beschreiben. Eine Zeile mit und bedeutet, dass der Knoten mit Knoten verbunden ist (und umgekehrt). Beachte, dass die Knoten nullbasiert indexiert sind. Sie sind also von bis nummeriert.
Ausgabe
Gib für den -ten Testfall “Case #t:” aus, gefolgt von einer Zahl, die Länge des kürzesten Weges von Knoten zu Knoten im -ten Graphen. Die Eingaben sind so gewählt, dass es immer ein Weg zwischen diesen beiden Knoten gibt.
Limits
Beispiel
Input:
2 7 8 0 1 2 0 0 3 1 4 2 4 5 3 4 6 6 5 7 7 0 1 2 1 2 0 4 0 4 3 5 3 5 6
Output:
Case #1: 3 Case #2: 4
Comment:
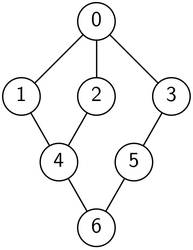
Bild 3: Illustration des ersten Beispiels.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Zusatzaufgabe: Überlege dir, wie du nicht nur die Länge des Weges sondern auch einen kürzesten Weg (als Abfolge von Knoten) ausgeben kannst.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Dijkstra
Mit Breitensuche lassen sich kürzeste Wege in Graphen finden, solange alle Kanten gleich lang sind. Häufig ist das jedoch nicht der Fall: Es kann zum Beispiel unterschiedlich lange dauern, von nach zu gelangen, wie von nach zu gelangen, obwohl es direkte Kanten von nach , sowie von nach gibt. In solchen Fällen geben wir jeder Kante zusätzlich ein Gewicht, welches diese zusätzliche Information beinhaltet.
In dieser Aufgabe geht es um Dijkstras Algorithmus zur Bestimmung von kürzesten Wegen in gerichteten Graphen mit nichtnegativen Kantengewichten.
Problembeschreibung
Gegeben ist ein gerichteter gewichteter Graph , das heisst einige Knoten , welche durch Pfeile/Kanten verbunden sind, wobei jeder Kante eine Zahl zugeordnet wird, ihr Kantengewicht. Wir stellen Kanten als Tupel dar, wobei und die Anfangs- und Endknoten der Kante sind und das Kantengewicht ist. Ein Weg von nach ist eine Reihe von Kanten . Das heisst, wenn man bei beginnt und dann der Reihe nach den Kanten folgt, erreicht man Knoten . Die Länge des Weges ist durch die Summe aller Kantengewichte gegeben: . Ein kürzester Weg von nach ist ein Weg von nach dessen Länge kleinstmöglich ist.
Wir wollen nun die Länge des kürzesten Weges zwischen zwei gegebenen Knoten bestimmen. Dies wird deine Aufgabe sein. Dijkstras Algorithmus kann verwendet werden, um dieses Problem effizient zu lösen, gegeben dass alle Kantengewichte mindestens sind.
(Dijkstras Algorithmus löst eigentlich sogar ein noch allgemeineres Problem: Er findet für einen gegebenen Startpunkt kürzeste Wege zu allen anderen Knoten. Er kann natürlich auch verwendet werden um für einen gegebenen Endpunkt kürzeste Wege von allen anderen Knoten her zu finden.)
Dijkstras Algorithmus
Sei die Länge des kürzesten Weges zwischen und . Eine Eigenschaft von kürzesten Wegen ist, dass
für
Hier machen wir einfach eine Fallunterscheidung über die letzte Kante auf dem kürzesten Pfad von nach . Falls eine gegebene Kante die letzte Kante auf dem kürzesten Weg von nach ist, dann ist einfach . ist dann die kleinste dieser Möglichkeiten.
Wir definieren falls es gar keinen Weg von nach gibt.
Für Graphen, die keine Wege von einem Knoten zu sich selbst haben, definieren die obigen Gleichungen bereits einen funktionierenden Algorithmus für die Berechnung von kürzesten Wegen, weil es keine zyklischen Abhängigkeiten zwischen Werten von gibt.
Im Allgemeinen gibt es aber solche zyklische Abhängigkeiten.
Dijkstras Algorithmus löst dieses Problem, in dem er für ein gegebenes für alle die Werte von in aufsteigender Reihenfolge berechnet. Es kann dabei dann natürlich vorkommen, dass nicht für jedes mögliche (in der zweiten Gleichung oben) der Wert bereits bekannt ist. Allerdings spielen diese Werte dann natürlich keine Rolle, weil sie wegen der geschickt gewählten Reihenfolge mindestens so gross sind wie . Hier verwenden wir die Annahme, dass alle mindestens sind.
Während jedem Zeitpunkt in der Ausführung von Dijkstras Algoritmus gibt es also einige Knoten für die wir bereits kennen, die bekannten Knoten und einige Knoten, für die dieser Wert noch nicht bekannt ist, die unbekannten Knoten. Ausserdem wissen wir, dass alle unbekannten Werte mindestens so gross sind wie jeder bekannte Wert.
Für jeden unbekannten Wert gibt es dann drei Möglichkeiten:
- für und ist bekannt.
- für und ist unbekannt.
- . (Falls von aus gar nicht erreichbar ist.)
(Merke, dass Möglichkeiten 1. und 2. sich nicht gegenseitig ausschliessen. Wieso?)
Dijkstras Algorithmus berechnet für alle mit bekanntem und unbekanntem den Wert als möglichen Kandidaten für den Wert von .
Die zentrale Beobachtung ist, dass der kleinste Kandidatenwert über alle solchen tatsächlich der korrekte Wert für das entsprechende ist.
(Das sollte intuitiv klar sein. Falls nicht, hier ein Beweis:
Es reicht zu zeigen, dass falls es erreichbare unbekannte Knoten gibt, es für mindestens einen unbekannten Knoten mit minimalem gelten muss, dass ein kürzester Weg zu ihm von einem bekannten Knoten aus über eine einzige Kante geht.
Beweis: Nimm an, dass die Behauptung nicht stimmt. Für jeden unbekannten Knoten hat mindestens ein kürzester Weg von zu ihm genau eine Kante zwischen bekannten und unbekannten Knoten. Schaue einen unbekannten Knoten mit minimalem an für den einer der solchen kürzesten Wege die kleinste Anzahl Kanten zwischen unbekannten Knoten hat. Nach Annahme gibt es auf dem Weg mindestens eine solche Kante. Sei der zweitletzte Knoten auf dem gewählten Weg. Dann ist und ein kürzester Weg von nach hat weniger Kanten zwischen Knoten mit unbekannten Werten als , ein Widerspruch.)
Dijkstras Algorithmus funktioniert wie folgt:
- Führe einen Kandidatenwert für Knoten ein.
- Solange es noch Kandidatenwerte gibt:
- Setze für den kleinsten Kandidatenwert , so dass der zugehörige Knoten ist, sowie noch nicht bekannt ist.
- Immer dann wenn ein neuer Wert bekannt wird, berechne Kandidatenwerte für alle mit .
Es folgt eine Implementierung in C++11:
#include <queue> using namespace std; #define OG(T) bool operator>(const T& o)const struct E{ int t,w; OG(E){ return w>o.w; } }; using VE=vector<E>; struct V{ VE in; bool v; }; using VV=vector<V>; using HE=priority_queue<E,VE,greater<E>>; int dijkstra(VV& g,int s,int t){ HE q; q.push({s,0}); while(!q.empty()){ E c=q.top(); q.pop(); if(g[c.t].v) continue; g[c.t].v=1; if(c.t==t) return c.w; for(auto&e:g[c.t].in) q.push({e.t,c.w+e.w}); } return -1; }
Der Graph wird dargestellt als ein vector<V>, wobei eine Instanz von einen einzelnen Knoten beschreibt: in ist ein vector<E> mit allen ausgehenden Kanten. v ist ein bool, welcher speichert, ob der Knoten bereits bekannt ist oder nicht. Eine Instanz von E beschreibt den Zielknoten t sowie das Kantengewicht w.
Wir verwenden eine priority_queue um die Menge der Kandidatenwerte zu verwalten. (Merke, dass die eingebaute priority_queue dummerweise standardmässig den grössten Wert zurückgibt anstatt den kleinsten.)
- q.push({s,0}) startet die Berechnung indem der Kandidatenwert 0 für Knoten s eingeführt wird.
- if(g[c.t].v) continue; verhindert, dass bereits bekannte Werte überschrieben werden. (Das ist notwendig. Wieso?)
- if(c.t==t) return c.w; gibt das Resultat aus, falls der Zielknoten gefunden wurde. An dieser Stelle könnte man z.B. auch die Werte von speichern.
- for(auto&e:g[c.t].in) geht über alle Kanten, die vom aktuellen Knoten weggehen.
- q.push({e.t,c.w+e.w}); führt neue Kandidatenwerte ein.
- In return -1; steht -1 für , also dafür, dass es keinen Weg von s nach t gibt.
Die Laufzeit dieser Version von Dijkstras Algorithmus ist , wobei die Anzahl Knoten und die Anzahl Kanten ist.
Aufgabe
Gegeben mehrere gerichtete Graphen mit nicht-negativen Kantengewichten, finde jeweils die Länge des kürzesten Weges vom ersten zum zweiten Knoten.
Eingabe
Auf der ersten Zeile steht die Zahl , die Anzahl Testfälle. Es folgen Zeilen mit jeweils den ganzen Zahlen , , sowie Trippeln von ganzen Zahlen (), welche Kanten von nach mit Gewicht beschreiben. Die Knoten sind von bis durchnummeriert.
Die Zahlen sind durch jeweils ein oder zwei Leerzeichen getrennt (siehe Beispiel).
Ausgabe
Gib für den -ten Testfall “Case #t:” aus, gefolgt von der Länge des kürzesten Weges von Knoten zu Knoten . Falls es von Knoten zu Knoten keinen Weg gibt, gib “Infinity” aus.
Limits
Beispiel
Input:
3 3 2 1 3 5 3 2 7 3 3 1 2 7 1 3 4 3 2 1 3 1 1 3 4
Output:
Case #1: 12 Case #2: 5 Case #3: Infinity
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Binäre Suche
Problem
Gegeben sei eine sortierte Liste von Zahlen (, , …, ). Wir wollen nun herausfinden, ob eine bestimmte Zahl in dieser Liste vorhanden ist. Falls in der Liste vorhanden ist, wollen wir zusätzlich die Position bestimmen.
Die triviale Lösung, die jede Position der Liste mit vergleicht, hat eine Laufzeit von (Diese funktioniert jedoch auch bei unsortieren Listen, wo die binäre Suche fehlschlägt). Mit der binären Suche können wir das Problem jedoch in lösen.
Lösung
Der Algorithmus der binären Suche ist Greedy und funktioniert nach dem Prinzip Teile und Herrsche.
Die folgenden Schritte wiederholen wir, bis die gesuchte Zahl gefunden wurde oder die Liste leer ist:
- Wir vergleichen die Zahl (mit , wobei für abrunden steht) in der Mitte der Liste mit , dabei können folgende Fälle auftreten:
- : Die Zahl ist gefunden. Wir können die Position berechnen und zurück geben.
- : Da kleiner ist als , muss vor sein, falls es in der Liste vorkommt. Wir können uns also auf die linke Hälfte beschränken.
- : Analog zum vorigen Fall können wir uns in diesem Fall auf die rechte Hälfte beschränken.
- Ist die neue Liste leer, kommt nicht in der Liste vor. Andernfalls beginnen wir mit der nun halbierten Liste wieder bei 1.
Am einfachsten schränken wir dazu die Liste durch einen oberen () und unteren () Index ein, die wir dann iterativ anpassen:
Seien A, N, X gegeben
Setze U = 1, O = N
Setze I = U+(O-U)/2
Solange U != O und A[I] != X
Falls A[I] > X
Setze O = I-1
Falls A[I] < X
Setze U = I+1
Setze I = U+(O-U)/2
Falls A[I] = X
"X ist an Position I in A"
Sonst
"X ist nicht in A"
Aufgabe
Gegeben eine monotone diskrete Funktion und ein y-Wert , finde den zu gehörigen x-Wert .
mit dem Definitionsbereich
Monoton bedeutet, dass die Werte der Funktion immer steigen (d.h. wenn man nach rechts geht, werden die Werte immer grösser). Die gegebene Funktion ist in jedem Fall monoton.
Wir betrachten nur diskrete Werte von , das heisst die abgerundeten Funktionswerte.
Werte von Funktionen berechnen
Wollen wir den Wert einer Funktion an einer bestimmten Stelle, z.B. berechnen, so setzen wir einfach den Wert () für ein und rechnen aus:
Beachte dass die -te Wurzel von ist: .
In Computerprogrammen geht das ausrechnen sehr einfach. Wir schreiben einfach eine Funktion, die den Wert ausrechnet, in C++ z.B. so:
double P(double x) {
return 2*pow(x, 1.0/2) + 3*x + 2*pow(x, 2);
}
Hinweis: die Funktion pow befindet sich in math.h. Beachte auch, dass du schreiben solltest und nicht . ist , denn die Division rundet bei Integern ab. Da ein Double ist, wird die Division mit Nachkommastellen durchgeführt.
Hinweis: die Funktion pow befindet sich in math.h.
Eingabe
Auf der ersten Zeile steht eine ganze Zahl , die Anzahl Testfälle. Für jeden Testfall folgt eine Zeile mit jeweils den Zahlen , , , , , , , , . Hierbei stehen:
- (Ganzzahl) für die obere Schranke des zu betrachtenden Definitionsbereichs von , die untere Schranke ist immer ,
- , , , , , , (Fliesskommazahlen) für die Koeffizienten der monotonen diskreten Funktion ,
- (Ganzzahl) für den gesuchten Funktionswert.
Ausgabe
Für den -ten Testfall gib eine Zeile “Case #t: X”, wobei ein zu gehöriger x-Wert, oder , falls die Funktion den Wert im vorgegebenen Bereich nicht annimmt.
Limits
Beispiel
Input:
2 10 0 0 0 0 1 0 0 4 10 0 0 0 0 1 0 0 6
Output:
Case #1: 2 Case #2: 0
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Präfixsumme
Problem
Es ist ein grosses Rechteck von Zahlen gegeben. Nun sollen für verschiedene Teilrechtecke die Summe aller Zahlen in diesem Teilrechteck berechnet werden. Betrachten wir zunächst den eindimensionalen Fall, bei dem man nur eine Liste mit Zahlen hat. Der offensichtliche Ansatz wäre, für jeden gefragten Bereich die einzelnen Zahlen zu addieren, also etwas in der Art:
for range in ranges: sum = 0 for i in range(range.start, range.end): sum += list_of_numbers[i] print(sum)
Dies ist jedoch für viele Anfragen zu langsam, da jede der Abfragen bis zu Operationen benötigt, der Algorithmus also in läuft.
Lösung
Statt für jede Abfrage viel zu berechnen, erstellen wir zu Beginn eine zweite Hilfsliste, die vorberechnete Werte enthält. Diese Werte erlauben uns dann, jede der Abfragen in konstanter Zeit () zu beantworten. Da wir die Berechnung der Hilfsliste nur einmal durchführen müssen, ist die Gesamtlaufzeit somit viel besser.
Nennen wir unsere Liste mit den Elementen , , , …, . Wenn wir nun unsere Hilfsliste - nennen wir sie mit den Elementen , , , …, - so berechnen, dass in gerade die Summe aller Zahlen der Liste bis und mit drin stehen, können wir die Summe des Bereichs von (inklusive) bis (inklusive) mit berechnen. Warum ist dies so?
Schauen wir uns z.B. den Bereich an. Die Summe die wir berechnen wollen ist also . Dann ist und . Rechnen wir nun , so ergibt dies . Dies ist genau die Summe, die wir suchen. Wir können also durch die Subtraktion die zu viel hinzuaddierten Elemente wieder “entfernen”.
Implementieren kann man das z.B. folgendermassen:
# vorberechnen b = [a[0]] for i in a[1:]: b.append(b[-1] + i) # Abfragen for range in ranges: if range.start == 0: print(b[range.end]) else: print(b[range.end] - b[range.start-1])
Das Vorberechnen können wir in durchführen und alle Abfragen in (da jede Abfrage in konstanter Zeit beantwortet werden kann). Somit verbessert sich unsere Lösung von auf .
Diese Idee kann nun einfach auf den zweidimensionalen Fall erweitert werden.
Ist nun das gegebene Rechteck mit Zahlen, so füllen wir das vorberechnete Rechteck jeweils mit der Summe des Teilrechtecks von der oberen linken Ecke bis zum aktuellen Feld. Dies kann man auf verschiedene Arten effizient berechnen. Eine Möglichkeit ist, das Rechteck von oben links durchzugehen und jeweils zu setzen. Die Subtraktion wird benötigt, da wir sonst dieses Teilrechteck doppelt zählen würden.
Nun kann die Summe des Teilrechtecks von bis ausgerechnet werden mit . Wir nehmen also wieder den zu grossen Bereich, der bis geht. Anschliessend ziehen wir den linken Bereich sowie den oberen Bereich ab, den wir zu viel hinzugezählt haben. Nun haben wir den Bereich bis jedoch zweimal abgezogen, weshalb wir ihn wieder hinzuaddieren.
Eingabe
Auf der ersten Zeile steht eine ganze Zahl , die Anzahl Testfälle. Für jeden Testfall folgen:
- eine Zeile mit , die Anzahl Spalten, Anzahl Zeilen und Anzahl Abfragen.
- eine Zeile mit . Dies definiert eine Folge mit . Die Folge startet beim gegebenen .
- eine Zeile mit . Dies definiert eine Folge mit . Die Folge startet beim gegebenen .
Das Rechteck ist nun gegeben durch .
Die Abfragen sind gegeben durch , , , , gesucht ist jeweils die Summe der Zahlen im Rechteck zwischen den Eckpunkten und , jeweils inklusive. Für die Abfrage () gilt , , und .
Die etwas komplizierte Eingabe verwenden wir, damit du nicht riesige Mengen an Daten herunterladen musst. Du kannst folgenden Code für C++ verwenden, um die Zahlen zu generieren:
struct range{ int startX, startY, endX, endY; range(int sx, int sy, int ex, int ey) : startX(sx), startY(sy), endX(ex), endY(ey){} }; void readInput(int& N, int&M, int& Q, vector<vector<int> >& field, vector<range>& queries){ cin >> N >> M >> Q; field.clear(); field.resize(M, vector<int>(N)); queries.clear(); int f0, a, c, m; cin >> f0 >> a >> c >> m; for(int y = 0; y < M; y++){ for(int x = 0; x < N; x++){ field[y][x] = f0; f0 = (f0 * a + c) % m; } } cin >> f0 >> a >> c >> m; for(int q = 0; q < Q; q++){ int r[4]; for(int i = 0; i < 4; i++){ r[i] = f0; f0 = (f0 * a + c) % m; } queries.push_back(range(min(r[0]%N, r[1]%N), min(r[2]%M, r[3]%M), max(r[0]%N, r[1]%N), max(r[2]%M, r[3]%M))); } } // in your code int N, M, Q; vector<vector<int> > field; vector<range> queries; readInput(N, M, Q, field, queries);
Ausgabe
Gib für jeden Testfall eine Zeile mit “Case #t:” aus ( ist die Nummer des Testfalls), gefolgt von leerzeichengetrennte Zahlen , die Summe der Zahlen in des Teilrechtecks .
Limits
Beispiele
Input:
2 7 2 7 67 56 86 101 62 34 71 71 5 3 8 31 28 65 79 2 15 48 79
Output:
Case #1: 298 216 140 290 445 86 126 Case #2: 40 493 277 275 339 372 151 129
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Ranking
| Rank | Username | Total (100) | dfs (20) | bfs (20) | dijkstra (20) | bsearch (20) | prefixsum (20) |
|---|---|---|---|---|---|---|---|
| loading ... |