Overview
Welcome to the Qualification Round of the Swiss Olympiad in Informatics! You will find below an overview of what you’ve done so far as well as a few things that you should know before getting started.
This contest is over.
| Category | Task | Total | Subtask 1 | Subtask 2 | Subtask 3 | Subtask 4 | Subtask 5 |
|---|---|---|---|---|---|---|---|
| Junior only | cheesemachine | ‒/100 | ‒/10 | ‒/13 | ‒/17 | ‒/26 | ‒/34 |
| Junior only | rotation | ‒/100 | ‒/10 | ‒/16 | ‒/11 | ‒/27 | ‒/36 |
| Both | landscaping | ‒/100 | ‒/13 | ‒/19 | ‒/17 | ‒/22 | ‒/29 |
| Both | trampoline | ‒/100 | ‒/8 | ‒/14 | ‒/29 | ‒/14 | ‒/35 |
| Both | train | ‒/100 | ‒/23 | ‒/15 | ‒/20 | ‒/16 | ‒/26 |
| Both | hikingsigns | ‒/100 | ‒/13 | ‒/15 | ‒/16 | ‒/27 | ‒/29 |
| Regular only | circuit | ‒/100 | ‒/20 | ‒/20 | ‒/20 | ‒/20 | ‒/20 |
| Regular only | cakeicing | ‒/100 | ‒/10 | ‒/15 | ‒/75 | ||
| Regular only | qrh | ‒/100 | ‒/25 | ‒/25 | ‒/25 | ‒/25 |
Cheese Machine
Binna designed a new machine to produce the best cheese throughout Mouseland. She is now testing it to make sure the cheese produced is in fact the best you can find before revealing the machine to the public. Each second, she notes down the results of her test: a number which combines the flavor of the cheese, the size of the cheese, the time elapsed since the machine was turned on, and the quantity of cheese produced. After gathering some amount of data, she would like to know if there is an anomaly in the results she received. If such an anomaly occurred, she would need to dismantle the machine to fix the issue. If no anomaly occurred, then the machine should be working correctly and she would like to predict the next result she should receive.
The machine’s output is easily predictable if the machine is working correctly. In fact, if everything works correctly, the machine’s result should always increase or always decrease by the same amount each second. An anomaly has occurred if the results Binna received don’t respect this rule at some point.
Knowing that, could you tell Binna if the machine produced an anomaly or, in the case no anomalies are detected, which result she should receive next?
Input/Output
All subtasks have the same input and output format.
Input
The first line contains the number of test cases . The test cases follow in the following format:
- The first line contains one positive integer , the number of second Binna ran her test.
- The second line contains integers, the -th one, , corresponding to the result she got after the -th second.
Output
For the -th testcase, output a single line:
- If an anomaly was detected, output Case #t: NO.
- If no anomalies were found, output Case #t: followed by , the predicted result Binna should receive next.
Subtask 1: A small test (10 points)
Binna only ran her test for two seconds because she didn’t want to stress her machine too much, and was eager to try the first wheel of cheese her machine produced.
Limits
Example
Input:
5 2 1 2 2 10 15 2 10 5 2 5 -5 2 42 42
Output:
Case #0: 3 Case #1: 20 Case #2: 0 Case #3: -15 Case #4: 42
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: Small test, no problems (13 points)
Binna improved her machine and assures you that no anomalies were produced during her test, but she only ran it for three seconds.
Limits
- No anomalies are present in the results.
Example
Input:
3 3 10 15 20 3 13 8 3 3 42 42 42
Output:
Case #0: 25 Case #1: -2 Case #2: 42
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Imprecise machine (17 points)
Binna didn’t like the taste of the cheese produced by her last machine. Unfortunately, her machine wasn’t perfect after all, even if she didn’t catch any anomalies. Because of an urgent meeting, Binna was once again only able to test her machine for three seconds before leaving. However, her test has a great chance to contain anomalies because of the bad taste.
Limits
Example
Input:
3 3 10 12 15 3 10 15 20 3 42 42 42
Output:
Case #0: NO Case #1: 25 Case #2: 42
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4: Finally a perfect machine (26 points)
Binna worked really hard on this new prototype and it now works perfectly. Thus, the test she ran doesn’t contain any anomalies. She also learned from her mistakes and ran the test for much longer than before.
Limits
- No anomalies are present in the results.
Example
Input:
4 4 9 12 15 18 5 10 15 20 25 30 3 9 7 5 2 42 42
Output:
Case #0: 21 Case #1: 35 Case #2: 3 Case #3: 42
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 5: The machine needs fixing (34 points)
Binna’s last machine was used so many times to produce cheese for the entire population of Mouseland that some parts broke. After fixing them, the machine unfortunately doesn’t work as well as before and may produce some anomalies when testing it.
Limits
Example
Input:
4 4 10 12 15 18 5 10 15 20 25 30 3 9 7 5 2 42 42
Output:
Case #0: NO Case #1: 35 Case #2: 3 Case #3: 42
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Rotation

Gouffre de Padirac sinkhole, Photo By Gerald Fauvelle - CC BY-SA 4.0.
Disaster strikes! Stofl was going for a hike in the rainforest when he fell down a sinkhole and ended up trapped in an underground tomb. In the center of the room there is a huge wheel with letters on it. Stofl can rotate the wheel however he likes as well as swap letters. Only once all the letters are brought into the correct position and the wheel is brought into the correct orientation will the door unlock. Stofl has found some clues on the walls but is not quite sure of the correct solution, so he would like to try out a few modifications and then check what letters are in specific positions on the wheel. Help him by writing a program that can simulate repeatedly rotating the wheel and repeatedly swapping two letters on the wheel and can answer his questions about what letter is currently located at a given position.
Formally the task can be formulated as follows: You are given a string consisting of lowercase letters and rituals. Each ritual is one of the following types:
- Print the -th character of .
- Swap the two characters at indices and in the string.
- Perform the following operation times in a row: delete the last character of and append it to the beginning (Rotate the wheel by ).
Input and Output
Input
The first line contains the number of test cases . test cases follow of the following format:
- The first line contains two integers, and , the length of the string and the number of rituals.
- On the second line is the string
- The next lines describe Stofl’s rituals. The first integer is the type of the ritual, which is either , , or .
- If the ritual is of type , a second integer follows, the index whose element that Stofl wants to query.
- If the ritual is of type , two integers and follow, the two indices whose elements Stofl wants to swap.
- If the rital is of type , a second integer follows, how far Stofl wants to rotate the wheel.
Visualization
Ritual type is performed transforming = “programming” into = “prmgramoing” ( and ):
Ritual type is performed transforming = “programming” into = “ngprogrammi” ():
Output
For the -th test case, print a line “Case #i:” followed by a string of lowercase letters where the -th character of the string is the answer to the -th ritual of type .
Subtask 1: No modifications (10 Points)
To make sure that you know what you are doing, Stofl wants to test you first whether you can accurately answer rituals whose answers he already knows, namely questions about the original, unmodified wheel. Therefore, in this subtask there are no rituals of types and .
Limits
- All rituals are of type
Example
Input:
3 3 4 soi 1 0 1 2 1 1 1 0 5 4 binna 1 1 1 0 1 2 1 4 5 6 mouse 1 0 1 4 1 0 1 1 1 2 1 3
Output:
Case #0: sios Case #1: ibna Case #2: memous
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: Small Wheel (16 Points)
Mouse Stofl has found another smaller wheel inside the tomb which must also be solved to open the door. As this one is easier, Stofl will solve this one first. He could do it on his own, but to reassure him of your programming skills (after all, his life is on the line), he still asks you to simulate his rituals and will give you questions to answer.
Limits
Example
Input:
2 3 5 pjp 3 2 2 1 2 1 0 1 1 1 2 6 14 mfegaw 1 5 3 0 1 5 3 0 2 4 5 1 2 2 0 3 1 3 3 4 3 2 3 3 3 5 1 1 1 0
Output:
Case #0: jpp Case #1: wwemaw
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: No rotations (11 Points)
Now assured that your program is correct, Stofl will start solving the large wheel. His strategy is to initially only swap some letters and only in later subtasks to rotate the wheel. Again, simulate his operations and answer his queries.
Limits
- There are no queries of type
Example
Input:
3 3 9 soi 1 0 1 2 1 1 1 0 2 0 2 1 0 1 2 1 1 1 0 5 7 binna 2 0 1 1 1 1 0 1 2 1 4 2 1 2 1 1 5 8 mouse 1 0 1 4 2 0 4 1 0 1 1 1 2 2 1 3 1 3
Output:
Case #0: siosisoi Case #1: binan Case #2: meeouo
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4: No swaps (27 Points)
Now that most letters are in the correct positions, Stofl must rotate the wheel into the correct orientation. As the wheel is very large, he can’t see most of the letters on the other side. Help him by again simulating the rotations he makes and answering his questions.
Limits
- There are no queries of type
Example
Input:
2 3 16 bul 1 0 3 1 1 0 3 1 1 0 3 1 1 0 3 0 1 0 3 1 1 0 3 1 1 0 3 1 1 0 3 0 5 6 stofl 3 2 1 0 1 1 1 2 1 3 1 4
Output:
Case #0: blubblub Case #1: flsto
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 5: Escape (36 Points)
To finish solving the wheel, Stofl will need you to be able to handle all three types of rituals.
Limits
Example
See Subtask 2.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Landscaping

A picture of a pyramid-shaped mountain in Bolivia
Still mesmerized by the pyramids Mouse Binna saw while participating at the MOI (Mouse Olympiad in Informatics) last year in Egypt, she concludes that the world needs more pyramids! Inspired by a picture of a pyramid-shaped mountain in Bolivia, Mouse Binna is determined to try and carve out such mountains herself once she gets there.
Having learned that simplification is a vital problem solving technique, Mouse Binna decides to make use of it here by modeling the terrain as a list of heights given as .
The goal is to form a pyramid out of the terrain by making it into a pyramid sequence. A pyramid sequence is defined as a list of integers of the form .
After wasting investing countless hours looking for the most efficient digging techniques, Mouse Binna concludes it is best to use a combination of two different landscaping methods.
- The first technique makes use of lots of explosive power (who would have thought) to blow the terrain down to the ground at some position. Being afraid of the dangers this method might entail, Mouse Binna decides to use it cautiously and only at either of the ends of the terrain, not somewhere in the middle. In terms of the list, this operation can be used to remove the first or the last element in current the array.
- The second technique, while quite a lot safer, certainly not as fun, uses a chisel to slowly dig away at a part of the terrain. In terms of the array, this operation decreases the height of the terrain by at some position .
Since Mouse Binna is ready to use all means necessary to create the best pyramid mountains, both operations can be performed any number of times. Can you help Mouse Binna by carving out the biggest pyramid mountains?
Subtask 1 (13 points)
Mouse Binna is looking at a hillside and wants to know whether it already forms a pyramid mountain, without applying any of the landscaping methods just yet.
Input
The first line contains the number of test cases . test cases follow in the following format:
The first line of the test case contains , the number of tiles. On the second line values follow, where the -th value is the height of the terrain at position .
Output
For the -th test case, output a line “Case #i: YES/NO” depending if the list of numbers forms a valid pyramid sequence.
Limits
There are test cases. In every test case, and .
Example
Input:
2 3 1 2 1 3 1 2 2
Output:
Case #0: YES Case #1: NO
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2 (19 points)
In this subtask, Mouse Binna wants to start carving up some mountains. To start of, however, she only wants to test out her first technique (the explosive one), i.e. you are only allowed to perform operations of type 1 on the list. Can you help her form the longest pyramid sequences?
Input
Same as subtask 1.
Output
For the -th test case, output a line “Case #i: l”, where is the length of the longest pyramid mountain that can be formed by landscaping.
Limits
There are test cases. In every test case, and . You are only allowed to perform operations of type 1.
Example
Input:
2 5 5 1 2 1 1 7 1 2 1 2 3 2 1
Output:
Case #0: 3 Case #1: 5
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3 (17 points)
Similar to the previous subtask, Mouse Binna now wants to try the second landscaping method. Or in other words, you are only allowed to perform operations of type 2 in this subtask.
Input & Output
Same as subtask 2.
Limits
Same as in subtask 2, but now you are only allowed to perform operations of type 2.
Example
Input:
2 3 1 2 2 5 1 2 3 4 1
Output:
Case #0: 3 Case #1: 5
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4 (22 points)
Being satisfied by the results from the previous tests, Mouse Binna now wants to use both techniques in conjunction to carve out the biggest pyramid mountains possible.
Input & Output
Same as subtask 2.
Limits
Same as subtask 2, but now you can perform operations of type 1 and 2.
Example
Input:
2 4 1 1 2 2 6 1 2 3 3 2 3
Output:
Case #0: 3 Case #1: 5
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 5 (29 points)
In this final subtask, Mouse Binna wants to apply her plans on even bigger mountains.
Input & Output
Same as subtask 2.
Limits
Same as subtask 4, but now .
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Trampoline
Mouse Stofl is going to visit an amusement park. He is very excited to go to his favorite attraction, the trampoline park.
There are trampolines in a line. Each trampoline has a jumpiness value associated with it. More formally, the -th trampoline has a jumpiness value of . Jumping on the -th trampoline will launch Stofl up and Stofl will land on exactly the -th trampoline, where Stofl will continue jumping, until he reaches the -th trampoline where he stops. All trampolines have a jumpiness except the -th one which has jumpiness . It is guaranteed that for all , meaning that Stofl will never jump past the last trampoline.
Input/Output
All subtasks have the same input and output format.
Input
The first line contains the number of test cases . The test cases follow in the following format:
- The first line contains one positive integer , the number of trampolines in the park.
- The second line contains integers, the -th one, , corresponding to the jumpiness of the -th trampoline.
Output
For the -th testcase, output a single line containing “Case #t: x” where is equal to the maximum number of trampolines Stofl can visit.
Subtask 1: From the beginning (8 points)
How many trampolines Stofl can visit if he starts at the first trampoline?
Limits
Example
Input:
3 3 2 1 0 3 1 1 0 5 1 1 2 1 0
Output:
Case #0: 2 Case #1: 3 Case #2: 4
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: From the optimal trampoline (14 points)
How many trampolines Stofl can visit if he selects the starting trampoline optimally?
Limits
Example
Input:
3 3 1 1 0 4 2 1 1 0 5 4 1 2 1 0
Output:
Case #0: 3 Case #1: 3 Case #2: 3
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: More trampolines (29 points)
The subtask is the same as subtask 2, but with more trampolines.
Limits
Example
Input:
3 3 1 1 0 4 2 1 1 0 5 4 1 2 1 0
Output:
Case #0: 3 Case #1: 3 Case #2: 3
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4: Adjusting one trampoline (14 points)
Stofl can choose the starting trampoline optimally, but he can also adjust the jumpiness of exactly one (any) trampoline with any jumpiness he likes.
Limits
Example
Input:
3 3 2 1 0 5 4 3 1 1 0 5 1 2 2 1 0
Output:
Case #0: 3 Case #1: 4 Case #2: 4
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 5: No limits (35 points)
The subtask is the same as subtask 4, but with more trampolines.
Limits
Example
Input:
3 3 2 1 0 5 4 3 1 1 0 5 1 2 2 1 0
Output:
Case #0: 3 Case #1: 4 Case #2: 4
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Train
Mouse Binna is a railway engineer. She is designing a straight railway line with stations, numbered . Each station has a level. Various trains will operate on this line. Some long-distance trains may only stop at major high-level stations, some local trains may stop at almost all stations.
There is a rule: if a train stops at station , it must also stop at all stations between its starting & terminal stations (inclusive) whose level is greater than or equal to the level of station .
For example, with the following levels of these stations, the IC, IR, RE, R trains comply with the rule. However, the “invalid train” doesn’t comply because it stops at station but not station which has the same level.

Subtask 1: Mini Railway Line (23 points)
Mouse Binna starts from designing a mini railway line.
Input
The first line contains the number of test cases . test cases follow in the following format:
- The first line contains two integers and , the number of stations and the number of trains.
- Each of the following lines contains an integer , followed by integers , the stations that the -th train stops, in ascending order.
Output
For the -th test case, output a line “Case #i: K”, where is the largest number mentioned above.
Limits
There are test cases. In each test case we have:
- for all
- for all
Example
Input:
2 4 2 3 0 1 3 3 0 2 3 15 6 3 0 1 14 5 0 1 3 8 14 10 0 1 2 3 4 5 6 8 12 14 9 6 7 8 9 10 11 12 13 14 4 5 6 8 9 4 0 1 2 4
Output:
Case #0: 1 Case #1: 5
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: Fixed Length Trains (15 points)
There are a considerable number of stations and trains. All the trains have starting station and terminal station .
Input
Same as Subtask 1
Output
Same as Subtask 1
Limits
There are test cases. In each test case we have:
- for all
- for all
Example
Input:
2 6 2 5 0 1 2 3 5 5 0 2 3 4 5 5 3 5 0 1 2 3 4 3 0 2 4 2 0 4
Output:
Case #0: 1 Case #1: 3
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Medium Railway Line (20 points)
There are a considerable number of stations and trains.
Input
Same as Subtask 1
Output
Same as Subtask 1
Limits
There are test cases. In each test case we have:
- for all
- for all
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4: Direct Trains (16 points)
There are a lot of stations and trains. All the trains are direct; in other words, they don’t have any intermediate stop except the starting and terminal station.
Input
Same as Subtask 1
Output
Same as Subtask 1
Limits
There are test cases. In each test case we have:
- for all
- for all
Example
Input:
2 6 6 2 1 2 2 1 4 2 2 3 2 3 4 2 2 5 2 2 4 5 2 2 1 2 2 1 2
Output:
Case #0: 4 Case #1: 2
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 5: Long Railway Line (26 points)
There are a lot of stations and trains.
Input
Same as Subtask 1
Output
Same as Subtask 1
Limits
There are test cases. In each test case we have:
- for all
- for all
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Hiking Signs
Mouse Binna has been appointed as director of tourism for Bolivia. She identified the lack of hiking infrastructure as one of the biggest problems and decided this to be the big point she wants to address. The nature is beautiful, there are plenty of interesting landmarks, and there already is a quite extensive road network.
The road network can be described as a set of intersections and a set of roads where each road connects exactly two intersections. The existing road network has the property that between any pair of intersections there is at most one path. Some of the intersections are especially beautiful and are called landmarks.
One piece of feedback Mouse Binna received is that mice can get lost in the wilderness. For that end, Mouse Binna decided to place hiking signs at each intersection. Each hiking sign shows a list of landmarks that can be reached and their respective distances.
Binna wants to build new roads in order to ensure the following:
- Each hiking sign should be unique. In other words, no two intersections should have the same set of reachable landmarks, and for each of those landmarks the same distance.
- Between any pair of intersections there is at most one path. This property was already present in the initial road network and Binna wants to keep it that way.
Is it possible to build new roads such that the constraint is satisfied? If yes, find a minimal set of roads that Binna needs to build.
Input and Output
All subtasks have the same input and output, and the same limits.
Input
The first line contains the number of test cases . The test cases follow in the following format:
- The first line contains three positive integers , and – the number of intersections in the network, the number of roads and the number of landmarks.
- The second line contains integers, the landmarks. The landmarks are guaranteed to be given in increasing order.
- The following lines describe the existing roads, each line consisting of two numbers and .
Output
For the -th testcase:
- If it is possible to build new roads to satisfy the properties, output Case #t: e, where is the minimal amount of roads you need to add. Then, print lines consisting of two numbers describing the roads you want to add.
- If it is not possible, output a single line with the words “Case #t: Impossible”.
Limits
In all subtasks we have:
- .
- .
- .
Subtask 1 (13 Points)
In this subtask we have . This means one can go from any intersection to any other intersection using a sequence of adjacent roads.
Input:
3 5 4 2 0 3 4 1 2 4 4 3 1 0 5 4 2 1 4 4 1 2 4 4 3 1 0 4 3 1 0 0 1 1 2 2 3
Output:
Case #0: 0 Case #1: Impossible Case #2: 0
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2 (15 Points)
In this subtask roads only connect intersections with index at most . (In other words for all edges .) Additionally all intersections larger than are guaranteed to be landmarks.
Input:
1 10 3 7 1 4 5 6 7 8 9 2 3 3 1 0 1
Output:
Case #0: 1 0 4
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3 (16 Points)
In this subtask any intersection has at most 2 adjacent roads.
Input:
4 3 1 1 1 1 2 3 2 1 1 0 1 1 2 5 2 2 1 3 0 1 1 2 6 0 1 1
Output:
Case #0: 0 Case #1: Impossible Case #2: 1 2 3 Case #3: 4 1 0 0 2 2 3 3 4
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4 (27 Points)
In this subtask all components of the road network contain at least one landmark.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 5 (29 Points)
No further constraints.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Circuit
Stofl is really tired of solving conventional tasks in Rust, so he decided to study circuits — a much simpler way of programming than the standard programming languages.
A program defining a circuit consists of several operations, where each operation is defined in the form X = Y op Z, where is a variable name for the new value, and reference some previously computed variables or constants, and op is a binary operation, which is restricted to +, - or max. Additionally, there is a special variable in, that represents a 2D-array of size that is being fed as an input to the circuit, and one special variable out, that represents the output of the circuit.
Below you can find an example circuit that computes the sum of the input elements, assuming and :
column1 = in[0][0] + in[1][0] column2 = in[0][1] + in[1][1] two_columns = column1 + column2 column3 = in[0][2] + in[1][2] out = two_columns + column3
There are the following restrictions for the circuits:
- Each variable name might only contain english letters, digits, underscores and square brackets and can not start with a digit and can not be longer than 50 characters.
- A variable might appear on the left side at most once.
- Any variable appearing on the right side must be defined before, or must reference an input element.
- Any constants used on the right side must be positive integers not greater than .
- Each circuit ends with an operation that has out on the left side.
Stofl already knows how to compute the sum of integer values using his favorite programming language, so to try out programming with circuits he decided to solve a different task. Given a 2D-array with integers from range , a cross is defined as any vertical segment intersecting any horizonal segment. Furthermore, a cross must contain at least one element of the array, i.e. a 0x0 cross is not allowed. An example of a cross can be found below:
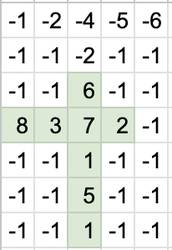
Stofl is interested in designing a circuit that computes the value of the maximum sum among all crosses in a given grid. Please help him to design it!
Input
The first line contains a single integer – the number of test cases. Then test cases follow, each of them contains one line with two integers and – the size of the grid (). Note that for a given subtask the input will never change and the values of and for each subtask is given in the corresponding section.
Output
For each test case, output a circuit that computes the maximum cross in a grid .
Example
Input:
2 1 1 1 2
Output:
Case #0: out = in[0][0] + 0 Case #1: max_single = in[0][0] max in[0][1] together = in[0][0] + in[0][1] out = max_single max together
Comment:
Scoring
This task has 5 subtasks. The score for each test case in each of those subtasks depends on the size of the circuit and its depth . The size is defined as the total number of operations (i.e. lines) in your circuit. Meanwhile, the depth is defined as the maximum distance between the out variable and any input variable in terms of operations. Or, in other words, if you were to substitute all the equations into one, the depth is the maximum amount of nested brackets. For example, in the second test case above the combined equation would look like this:
out = (in[0][0] max in[0][1]) max (in[0][0] + in[0][1])
which gives a depth of 2. The score for such a circuit will then be given according to the following snippet (no closed formula as we are not at the math olympiad here, formulas are overrated anyways):
double get_score(double ratio) const { return min(1.0, 0.3 + 0.7 * ratio * ratio); } double score(int n, int m, double depth, double size, int max_score) const { double S = get_score(expected_size(n, m) / size); double D = get_score(expected_depth(n, m) / depth); return S * D * max_score; }
The values of expected_size and expected_depth for all the inputs are specified in the subtask sections. Then, the score for a test is defined as the minimum score across all test cases. If your circuit is not valid (i.e. contains syntax errors or is not correctly computing the maximum sum among all crosses), you will get Wrong answer and therefore 0 points for the entire subtask.
Subtask 1 (20 points)
- All integers in the grid are guaranteed to be positive.
Scoring Parameters
| expected_size | expected_depth | ||
|---|---|---|---|
| 1 | 63 | 62 | 5.98 |
| 1 | 101 | 100 | 6.66 |
| 1 | 128 | 127 | 7 |
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2 (20 points)
- It is guaranteed that the given array will be a prefix (possibly with size 0) of only negative integers, followed by only positive integers, i.e. the array is of the form: -, -, ..., -, +, +, ..., +. It is guaranteed that the array always contains at least one positive integer.
Scoring Parameters
| expected_size | expected_depth | ||
|---|---|---|---|
| 1 | 63 | 93 | 8.97 |
| 1 | 101 | 150 | 9.99 |
| 1 | 128 | 190.5 | 10.5 |
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3 (20 points)
Scoring Parameters
| expected_size | expected_depth | ||
|---|---|---|---|
| 1 | 63 | 279 | 8.97 |
| 1 | 101 | 450 | 9.99 |
| 1 | 128 | 571.5 | 10.5 |
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4 (20 points)
- All integers in the grid are guaranteed to be positive.
Scoring Parameters
| expected_size | expected_depth | ||
|---|---|---|---|
| 53 | 51 | 7800 | 12.84 |
| 73 | 37 | 7776 | 13.19 |
| 128 | 128 | 48387 | 15.75 |
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 5 (20 points)
- No additional constraints.
Scoring Parameters
| expected_size | expected_depth | ||
|---|---|---|---|
| 53 | 51 | 52000 | 34.28 |
| 73 | 37 | 51840 | 35.67 |
| 128 | 128 | 322580 | 42 |
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Cake icing
The Game
Binna and Stofl both have a pot with ml of Icing. For each pour, they can fill some part of the remaining icing into the jar. The amount of icing must be equal to , where is the amount of pieces in the pour and the thickness.
At the end of the game, the importances of all pieces with the icing of a mouse get added. The sum counts as the score for this mouse.
Protocol
The program communicates with the grader over stdin / stdout.
- ‘U’ upwards, to (, )
- ‘D’ downwards, to (, )
- ‘R’ to the right, to (, )
- ‘L’ to the left, to (, )
The jar is not allowed to go off the cake.
When it’s the opponents turn, your program gets the pour the opponent made in the same format.
A program should print a pour with and strictly positive if it can’t or does not want to pour. However, this still counts as one of its turns.
Limits
These limits hold for all possible maps. They are thus too loose for the majority of map configurations. More details about the map configurations are in the section Maps.
Beispiel
Open the example in the visualization
The cake in the beginning of the game. The importances are represented as black squares. The bigger the square, the greater the importance.
The cake after the first pour of the orange mouse. Three pieces were iced with thickness 7.
The cake after the first pour of the blue mouse. The piece at the bottom left was iced with thickness 8 and now has the blue icing, because 8 > 7.
The cake after the second pour of the orange mouse. The piece at the bottom right was iced with thickness 2.
The cake after the second pour of mouse blue, at the end of the game. Mouse blue iced all the pieces at the right with thickness 3. The piece at the bottom right now has the blue icing (3 > 2), but the piece in the middle right stays orange (3 <= 7).
Here is the communication from the perspective of the orange mouse. The input of the program is marked with “<”, the output with “>”.
< 2 3 3090 2 < 8 166 < 558 706 < 753 430 < Y > 1 1 7 3 > L D < 0 0 8 1 < > 1 0 2 1 > < 1 0 3 3 < U U
Creativity platform
The creativity task will take place on the creativity platform. There you can create new bots, upload the source code for your bots, play games against other participants (or your own bots), view the results of tournaments, and see a ranking of all bots. If you have any questions about the platform do not hesitate to ask us.
A few notes about the platform:
- The idea is that you create a new bot for a completely new strategy. For small updates to your current strategy just upload a new version for the appropriate bot. There is no hard limit on the number of bots you can create, but we ask you to keep it to a reasonable number.
- You can not choose the name of your bots. This is to provide some anonymity and we hope that this encourages everyone to play games against each other more freely. If you are unhappy with the name of your bot you can randomize it again as long as you did not yet upload any code.
- By default, no one can play games against your bots. We think it is very helpful to already play some games before the tournaments and compare your bot with other bots. In order for there to be bots to compare against, some people need to allow others to play games against their bots. So please set your bots to accept games if you feel comfortable doing so. There is also the option where you have to confirm every game so you have better control over which bots you want to play against.
- If you have bots which require confirmation to play against, don’t forget to check from time to time whether you got any requests.
- Don’t forget to register your best bot for the tournaments. You can only register one bot per tournament.
- The time limit for a bot is 4 seconds per game.
- If you submit a Java bot, your main class needs to be called and it may not be in any package.
Subtask 1: Play by the rules (10 Points)
Write a bot that follows the rules and can beat the example bot. Just play and win any game against the random bot on the creativity platform. Games that are part of a tournament don’t count for this subtask. We have to manually update the scores, so it might take a few days until they show up on the qualification round ranking.
Subtask 2: Play smart (15 Points)
Write a bot which is able to beat our smart bot. Play and win games on at least 5 different map layouts against the smart bot on the creativity platform. You may choose the other map parameters freely. Games that are part of a tournament don’t count for this subtask. We have to manually update the scores, so it might take a few days until they show up on the qualification round ranking.
Subtask 3: Tournaments (75 Points)
You play against other participants of SOI in multiple tournaments. Based on the rankings of these you will get points.
Each tournament is worth a certain amount of points and you will get a fraction of these based on your rank: 100% for rank 1, then 10% less for every following rank until rank 6 (50%), then 5% less for every following rank. Some of the bots are not from participants, so the points you receive might not match the displayed ranking.
In the end, your score for this subtask will be the maximal score you achieved during any tournament. There will be the following tournaments:
- 25.9.2024, 20:00: Early bird tournament, worth 20 points.
- 9.10.2024, 20:00: Getting started tournament, worth 30 points.
- 23.10.2024, 20:00: Midway tournament, worth 40 points.
- 6.11.2024, 20:00: Getting serious tournament, worth 50 points.
- 20.11.2024, 20:00: Final spurt tournament, worth 60 points.
- 1.12.2024, 10:00: Creativity tournament, worth 75 points. Ranking will be hidden.
We will update the scores on the qualification round ranking after every tournament, but as we do this manually it might take a few days.
The Creativity tournament does not count for the qualification. The results will be hidden until the SOI-Camp. In the SOI-Camp we will present the results and award the winner with a prize. The maximum number of points one can get from this task for Qualification is thus 85.
On the creativity platform you can view additional details about the tournaments. A tournament consists of multiple map configurations. For each configuration you will play against every other bot. For a win on a map you will get , for a draw and for a loss score. The ranking will be according to the sum of these scores across all played games.
Maps
There are a few map configurations on which we will run the bots. A configuration consists of the following parameters:
- Cake size:
- small:
- medium:
- large:
The number of pieces with importance larger than zero will be noted as .
- Icing amount: How much ml of icing will be in the pot in the beginning:
- little:
- medium:
- much:
- Pours: How many pours each mouse is allowed to make:
- few:
- medium:
- many:
- Centralness: How evenly the importances are spread over the pieces:
- spread:
- medium:
- concentrated:
Hints
It is important for interactive tasks to flush the output buffer after every turn to make sure the server can see your output.
Use the following commands:
- C/C++: fflush(stdout);
- C++: cout << flush; (not necessary if you read afterwards)
- There are similar commands in other languages.
Furthermore it is important that you don’t wait for more characters than the server gives you as an input. For example spaces or line endings in C format strings are a common source for errors. For example if you read the last variable in the input with “scanf("%d ", &x);” it will wait for the next character that is not a space or a line break. You will receive such a character only after you printed your next turn. To solve this use “scanf("%d", &x);” instead (no non-printable characters after the “%d”).
Additional Tools
If you want to run your bots locally you can download the judge and the visualization here. This also includes a sample C++ bot. There is a short explanation on how to run the judge and visualization included. They are the exact same version which is used on the creativity platform.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
QRH
The homework part of the qualification round (QRH) consists of 4 tasks, each of which is worth 25 points. You can gain a maximum of 100 points counting towards your score of the regular round.
QRH GraderThis helps you get familiar with our grading system which we will use in all our events after the qualification round, including workshops, camp, finals, and team selection.
You can submit in C++ (recommended), Java or Python.
| C++: | If you don’t have a setup already, we recommend installing VSCode. |
|---|---|
| Java: | Read Java on the SOI Grader. |
| Python: | Read Python on the SOI Grader. |
For QRH you can discuss solutions with friends or publicly on Discord, as long as you don’t share source code. We are also happy to help you! If you need help with the grading system or have questions regarding the theory or tasks, don’t hesitate to ask here or in Discord.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Junior Ranking
| Rank | Username | Total (600) | cheesem… (100) cheesemachine | rotation (100) | landsca… (100) landscaping | trampoline (100) | train (100) | hikings… (100) hikingsigns |
|---|---|---|---|---|---|---|---|---|
| loading ... |
Regular Ranking
| Rank | Username | Total (700) | landsca… (100) landscaping | trampoline (100) | train (100) | hikings… (100) hikingsigns | circuit (100) | cakeicing (100) | qrh (100) |
|---|---|---|---|---|---|---|---|---|---|
| loading ... |