Overview
This contest is over.
| Task | Total | Subtask 1 | Subtask 2 | Subtask 3 | Subtask 4 | Subtask 5 |
|---|---|---|---|---|---|---|
| cablecar | ‒/100 | ‒/10 | ‒/20 | ‒/30 | ‒/40 | |
| gotthard | ‒/100 | ‒/20 | ‒/20 | ‒/40 | ‒/20 | |
| matryoshka | ‒/100 | ‒/10 | ‒/20 | ‒/20 | ‒/20 | ‒/30 |
| waterslide | ‒/100 | ‒/20 | ‒/20 | ‒/20 | ‒/40 | |
| salesman | ‒/100 | ‒/20 | ‒/10 | ‒/10 | ‒/60 | |
| racing | ‒/100 | ‒/20 | ‒/30 | ‒/50 | ‒/0 |
Cablecar
Mouse Stofl passionately likes riding the cable car. To be able to enjoy the cable car even at home, he bought a small cable car model. The view from a cable car can be enjoyed optimally if the cable car’s ride is uniform. This is the case if and only if the slope of the rope is the same at each point of the ride – otherwise, the cable car would start swinging, an event that Stofl would like to avoid. He has measured the heights of his pillars and now needs your help to build his cable car out of them.
All pillars are installed on the floor, which has the same elevation everywhere. The bottom and top stations can be installed at an arbitrary height. After Stofl has installed the the pillars, he will install them suitably, such that the slope remains uniform.
Subtask 1: Small Cable Car (10 Points)
The cable car has already been built by Stofl. There are exactly 3 pillars, which are installed in distances of 1. Help Stofl to decide if the view can be enjoyed or not.
Stofl does not only want to build a model cable car, but of them. Each of those cable cars has its own pillars and is independent of the others.
Input
The first line contains the integer , the number of cable cars that Stofl would like to build.
For each of those cable cars, a description of its pillars follows, which is formatted as follows: On the first line there is given the integer , the number of pillars (always 3) and on the second lines there are integers, the heights of the pillars.
Output
For the -th of the cable cars, print “Case #t: yes” if the view can be enjoyed optimally. Otherwise print “Case #t: no”.
Constraints
- For the number of test cases, we have .
- For the number of pillars, we have .
- For the heights of the pillars, we have .
Example
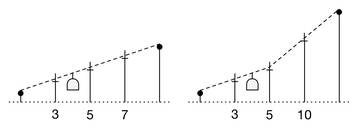
Sample input for subtask 1.
Input:
2 3 3 5 7 3 3 5 10
Output:
Case #1: yes Case #2: no
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: Long Cable Car (20 Points)
While you solved the first subtask, Mouse Stofl bought an extension kit for his cable car. Equipped with this kit, he now has pillars to dispose. He picks of them and installs them as in Subtask 1. Again, help Stofl to figure out whether the view can be enjoyed.
Input
As for subtask 1, but is not necessarily equal to
Output
As in subtask 1.
Constraints
- For the number of test cases, we have .
- For the number of pillars, we have .
- For the heights of the pillars, we have .
Example
Input:
3 8 1 2 3 4 5 6 7 9 2 1 5 4 20 15 10 5
Output:
Case #1: no Case #2: yes Case #3: yes
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Find an Enjoyable Part (30 Points)
Mouse Stofl has installed pillars, again equally spaced. As Stofl has a lot of room, he built a long row of pillars. Now he wants to find the longest part of this row that can be used to build a cable car from which the view can be enjoyed optimally. As Stofl is lazy, he does not want to move any pillar. Therefore, the enjoyable part should be contiguous. Help Stofl to find the longest contiguous enjoyable part.
Input
As in subtask 2.
Output
For the -th of the cable cars, print “Case #t:”, followed by a single number which is the length of the longest contiguous enjoyable part.
Constraints
- For the number of test cases, we have .
- For the number of pillars, we have .
- For the heights of the pillars, we have .
Example
Input:
2 10 2 3 10 11 12 13 14 15 16 500 5 3 20 25 30 35
Output:
Case #1: 7 Case #2: 4
Comment:
Case #1: Stofl chooses the contiguous part between the pillars of heights 10 and 16.
Case #2: The longest enjoyable part is between the pillars of heights 20 and 35.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4: Removing Pillars (40 Points)
After Stofl has played around with the cable car from subtask 3 long enough, he would like to build a new one. He has, again, installed all pillars in a row. However, now he is willing to remove some of the pillars. After he has removed some pillars, he moves the remaining pillars back together, so that they are equally spaced again. Help Stofl remove the smallest number of pillars, such that the remaining pillars can be used to form the longest cable car possible, under the constraint that the view can be enjoyed optimally.
Input
As in subtask 3.
Output
For the -th of the cable cars, print “Case #t:”, followed by a single number , which is the minimum number of pillars that Stofl has to remove such that the view is optimal.
Constraints
- For the number of test cases, we have .
- For the number of pillars, we have .
- For the heights of the pillars, we have .
Example
Input:
2 5 100 200 300 400 500 7 22 24 25 26 100 28 30
Output:
Case #1: 0 Case #2: 2
Comment:
Case #1: Stofl does not need to remove any pillars, as they already form a cable car with an optimal view.
Case #1: Stofl removes the pillars with heights 25 and 100.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Gotthard Tunnel
End of December 2016, the new Gotthard Base Tunnel will be completed. Now, a building inspector visits the tunnel and observes that the floor and roof where built in an irregular fashion. The differences can even be so large, that it is not possible to see straight through the tunnel. (I.e. there is no horizontal line passing the tunnel such that it never crosses nor touches the roof or floor of the tunnel.) The inspector is able to measure the line of sight from his position at an arbitrary height (I.e. the height of the floor and the size of the inspector do not matter), it should, however, be oriented horizontally. On both sides of the tunnel, there is a closed door which covers the entire height of the tunnel and blocks sight. The doors are located right before the first, and right after the last given position, respectively.
The inspector now wants to analyze the irregularities and clean them up where necessary. To complete this task, he has planned to complete the following four subtasks. Help him to solve them!
Input
The input is given in the same format for all subtasks: On the first line, there is a number , describing the number of test cases.
After that, there follow three lines for each test case:
- On the first line, there is a single nonnegative integer , the length of the tunnel in meters.
- One line consisting of integers follows, the respective elevations above sea level of the roof at position .
- One line consisting of integers follows, the respective elevations above sea level of the floor at position .
The position is the northmost position, the southmost.
Output
In all subtask, for each test case you should find a certain distance . For each test case, print a line in the format Case #i: D, where is the number of the test case (for the first test case we have ), and is the required distance.
Subtask 1: Stationary (20 Points)
The building inspector stands at the door on the north and would like to know how far he can see into the tunnel.
Constraints
Examples
Input:
1 4 7 9 6 8 6 2 1 5
Output:
Case #1: 2
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: Short Walk (20 Points)
The inspector passes through the tunnel and would like to know, what the maximum distance which he can see during his walk is.
Constraints
Examples
Input:
1 7 7 9 6 8 7 9 8 6 2 1 5 4 3 7
Output:
Case #1: 5
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Long Walk (40 Points)
This subtask is identical to subtask 2, but the tunnel is allowed to be significantly longer now.
Constraints
Examples
Input:
1 15 7 9 6 8 7 9 8 7 9 6 8 7 9 8 7 6 2 1 5 4 3 6 6 2 1 5 4 3 6 6
Output:
Case #1: 6
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4: Clearing the Tunnel (20 Points)
The tunnel should be improved to a state where it is possible to see one end from the other and thus is able to route the rails straight through horizontally. To this end, one removes obstacles ranging too far into the tunnel from the roof and the floor. (Any pits left after this procedure are filled during a later step, which is not interesting to us now.) However, the total horizontal distance which is traveled during this step should be kept at a minimum to keep costs low. The inspector would like to know the minimum distance the two construction crews need to travel in total (i.e. we consider the sum of both distances), until there exists a horizontal line of sight.
Constraints
Examples
Input:
2 15 8 7 6 8 9 5 8 7 4 6 8 9 7 8 7 6 2 3 4 1 2 1 3 1 2 5 3 5 6 4 9 8 7 5 6 8 9 4 8 7 6 4 3 4 5 1 2 1 2
Output:
Case #1: 8 Case #2: 5
Comment:
Case #1: From the north (left), the building crew needs to travel just 1 meter far into the tunnel, however, the building crew from the south (right) needs to travel 7 meters, which is 8 meters in total.
Case #2: In this case, only the crew in the north (left) needs to work, in a segment of length 5 meters.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Matryoshka
Mouse Dimitri gave Mouse Stofl some packages containing different Matryoshka dolls as a present. Matryoshka dolls are wooden colourful pear-shaped Russian dolls that can be nested inside each other.

Matryoshka series
As Dimitri isn’t very tidy, dolls of different Matryoshka-sets are mixed together. That is why it is not necessarily the case that all dolls can be nested within each other. A doll can be put inside another if its height and its width are both strictly smaller.
Subtask 1: One Matryoshka-set (10 points)
Dimitri has put the Matryoshka dolls into packages. Stofl opens the packages one by one and tries to nest all dolls that were in the same package into each other. Write a program that tells Stofl if all dolls within one package can be nested within each other.
Input
The very first line of input contains the number of packages . For each package the are three lines of input. The first line contains the number of dolls . The second line contains numbers, signifying the widths of the Matryoshka dolls. The third line contains numbers, signifying the corresponding heights of the Matryoshka dolls.
Output
For the -th package output Case #i: followed by YES if all dolls can be put into each other, or NO respectively if they cannot be nested.
Limits
- For the number of packages it holds that .
- For the number of dolls per package it holds that .
- For the widths and heights it holds that .
Example
Input:
2 3 1 2 3 1 2 3 3 1 2 3 1 3 2
Output:
Case #1: YES Case #2: NO
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: Largest Matryoshka-set (20 points)
As Stofl is a very curious Mouse he would like to know what the maximum number of dolls that can be nested together. As before he only considers one package at a time. Help Stofl find the answer!
Input
The same format as in subtask 1.
Output
As output we expect the package number and the maximum number of dolls that can be nested in each other. Use the following format: Case #i: Z.
Limits
- For the number of packages it holds that .
- For the number of dolls per package it holds that .
- For the widths and heights it holds that .
Example
Input:
2 7 1 2 3 4 5 6 7 1 5 6 2 3 4 7 4 1 1 1 2 1 1 1 2
Output:
Case #1: 5 Case #2: 2
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Many dolls (20 points)
A few day after getting the packages Stofl receives a letter from Dimitri, asking for help. Dimitri discovered many more Matryoshka dolls in his Grandmother’s attic. Now he would also like to know the maximum number of dolls he can nest in each other. Dimitri suspects that your solution to subtask 2 may be too slow.
Input
The same as in subtask 1.
Output
The same as in subtask 2.
Limits
- For the number of packages it holds that .
- For the number of dolls per package it holds that .
- For the widths and heights it holds that .
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4: Group photo (20 points)
Stofl is very happy about his Matryoshka dolls and would really like to post a photo of them on Instagram. Unlike Dimitri Stofl is very tidy, so he has the following rule for placing the dolls in for his photo: In front of every Matryoshka doll Stofl starts a new row of smaller Matryoshka dolls that will be placed next to each other. The height of every doll in that row must be smaller than the doll behind them and the width of the row, which is equal to the sum of all the widths of dolls in the row, must be strictly smaller than the width of the doll behind it. Stofl then applies the same procedure on every new doll until he cannot place any more dolls.
Stofl chooses one single Matryoshka doll to start with before applying his procedure. As Stofl has received many dolls of the same size, you may assume that the input specifies Matryoshka-types which can be used as often as you want. Also measurements show that no two Matryoshka-types have exactly the same height or exactly the same width.
Input
The same as in subtask 1.
Output
For each package in the input output the photo number and the maximal number of dolls that Stofl can fit in one photo if he starts with a single doll. Use the format Case #i: Z.
Limits
- For the number of packages it holds that .
- For the number of Matryoshka-types per package it holds that .
- For the widths and heights it holds that .
Examples
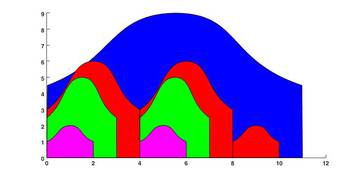
Example 1
Example 2
Example 3
Input:
3 7 2 3 4 6 8 10 11 2 5 6 1 3 4 9 2 1 100 1 2 4 14 3 4 5 14 3 4 5
Output:
Case #1: 8 Case #2: 100 Case #3: 8
Comment:
In a frontal photograph this can be described as followes:
The big blue 11x9 Matryoshka doll is placed at the back. In front of it we places a row consisting of two 4x6 dolls and one 2x2 and thus uses the maximally allowed width. In front of every doll in the red row Stofl now proceeds to place a new row. This is only possible for the 4x6 dolls, as there is no doll that is smaller than 2x2. The two new rows consist of a single 3x5 doll and are coloured green. In front of each of these a new pink row consisting of a single 2x2 doll is placed. Thus we have reached the final placement which means there will be a total of 8 Matryoshka dolls on the photo.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 5: Group photo 2 (20 point)
Dimitri, who has discovered Stofl’s photos, would like to show that he too can be tidy on the one hand and on the other hand would also like to that there are even larger Matryoshka dolls. Dimitri uses the same procedure as Stofl did in subtask 4 to place his dolls for the photograph. As before Dimitri is impatient and would like you to write a fast solution, so you may need to optimise your program from subtask 4.
Input
Same as in subtask 1.
Output
Same as in subtask 4.
Limits
- For the number of packages it holds that .
- For the number of Matryoshka-types per package it holds that .
- For the widths and heights it holds that .
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Waterslide
Mouse Stofl likes to ride water slides. His favourite amusement park features a large network of slides connecting small pools. At each pool, there is a ladder which can be climbed to reach some number of other slides. To prevent collisions, only one slide finishes per pool.
Mouse Stofl starts from one pool and would like to have as much fun as he can. He has most fun if he can ride as many distinct water slides as possible without ever walking between two pools. Can you help him determine such a maximum enjoyable sequence of slides? Note that Stofl is allowed to ride the same slide multiple times, although this wouldn’t increase his pleasure.
Subtask 1 (20 Points)
Help Stofl find the number of distinct slides on a maximum enjoyable sequence if he wants to start from a given pool.
Input
There are multiple test cases. The first line of the input contains the number , which indicates the number of test cases. test cases follow.
A single test case starts with two numbers and on separate lines (). The pools are numbered from to . is the total number of pools and indicates the starting pool. lines follow, which describe the pools in order. Each of these lines contains the number of pools that can be reached from the described pool by going down a single slide, followed by the numbers of those pools. While each pool can have an arbitrary number of outgoing slides, it is guaranteed that there is exactly one slide leading to it.
Output
For each test case you should output “Case #t:”, where is the number of the case, starting from one. On the same line, one number should follow: The maximum number of distinct slides Stofl can visit without walking between two pools.
Constraints
- We have .
Example
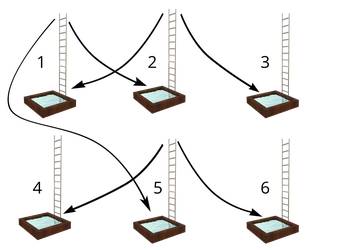
First test case of sample input visualized.
Input:
3 6 1 2 2 5 2 1 3 0 0 2 4 6 0 6 3 1 2 1 3 1 4 1 5 1 6 1 1 6 2 1 1 1 2 1 4 2 3 5 1 6 0
Output:
Case #1: 4 Case #2: 6 Case #3: 1
Comment:
Case #1: The best sequence of platforms is either or . Note that in this example, Stofl has to visit a platform twice to have the most fun.
Case #2: The best sequence of platforms is . Stofl can visit every platform because they are connected in a loop.
Case #3: The best sequence of platforms is . In this example, Stofl is trapped on a platform which is only connected to itself. Thus he can’t reach any of the other platforms.
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2 (20 Points)
The starting pool can now be chosen by Stofl himself. Your task is to find the number of distinct slides on a maximum enjoyable sequence starting from any of the pools. In the input format, is therefore omitted now.
Example
Input:
2 6 2 2 5 2 1 3 0 0 2 4 6 0 6 1 1 1 2 1 4 2 3 5 1 6 0
Output:
Case #1: 4 Case #2: 4
Comment:
Case #1: The best sequence of platforms is either or .
Case #2: The best sequence of platforms is . Stofl can avoid the loops at platform one and two and instead chooses the interesting ride from platform three to six.
Constraints
- We have .
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3 (20 Points)
In anticipation of even more fun, Stofl decided to visit an even larger amusement park, featuring nearly one million unique pools. Stofl is still allowed to choose the starting pool.
Constraints
- We have .
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 4 (40 Points)
This is a theoretical subtask, you do not have to provide any source code. Submit a proof that your solution to subtask 2 and/or 3 is correct (see guide) including an asymptotic analysis of the algorithm’s runtime and memory usage.
The contest is over, you can no longer submit.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Salesman
Maus Stofl has seen enough of Switzerland and plans to emigrate to Russia to become a traveling Salesman. In the countryside north of Kasan, where this year’s IOI takes place, are N villages. Every village is connected with every other village and Stofl has to travel a certain distance to get from one village to another.
Stofl is overwhelmed by the cultural diversity of Russia and wants to experience as much as possible. For this reason he always chooses the village as far away as possible from the current village until he has visited all villages while never visiting a village twice. If he can choose from multiple villages with the same distance to go next, he chooses one by chance. Stofl comes to know of another traveling salesman, Mouse Vladimir. Mouse Vladimir has the same strategy as Stofl with the exception that he always goes to the village with the shortest distance because he already knows the environment and wants to finish as fast as possible.
Subtask 1: Calculate Paths (20 Points)
Mouse Stofl starts in village and mouse Vladimir starts in village . Calculate how far they have to travel until they visited all villages.
Input
The first line contains an integer , the number of test cases.
For each test case, the first line contains three integers , and , corresponding to the number of villages, the initial starting village of Stofl and the starting village of Vladimir. lines with integers each follow, where is the -th number on the -th line and stands for the distance between the -th and the -th village. All distances are pairwise distinct, i.e. no two distances between different villages are equal.
Output
For the -th test case, display a single line “Case #t: S V”, where is the distance that mouse Stofl travels and the distance of mouse Vladimir.
Constraints
Example
Input:
1 4 1 1 0 1 5 6 1 0 2 10 5 2 0 14 6 10 14 0
Output:
Case #1: 22 17
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2a: Example with Different Distances (10 Punkte)
Mosue Stofl wants to know if it is possible to choose the distance between the villages in a way that the total distance of Stofl is exactly longer than the distance of Vladimir. Note that as previously, all distance are pairwise distinct.
Input
The first line contains an integer , the number of test cases.
For each test case, there are given two integers: the number of villages and the difference between Stofl’s and Vladimir’s distances .
Output
For the -th test case, the first line has the format “Case #t: N A B”. the same as given in the input, and correspond to the starting villages of Stofl and Vladimir. lines with integers each follow: The -th number on the -th line is the distance between the villages and . Note that all distance have to be distinct and the distance has to be the same in both directions (i.e. ). The distance of a village to itself has to be (i.e. ). For it should hold .
Constraints
Example
Input:
1 4 5
Output:
Case #1: 4 1 1 0 1 5 6 1 0 2 10 5 2 0 14 6 10 14 0
Comment:
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2b: Example with Equal Distances (10 Points)
Now Stofl wants to know if it is also possible for . Input and output are the same as in subtask 2a.
Constraints
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3 (60 Points)
In general, the distances between two villages don’t have to be different. If there are ties for the shortest/farthest away village, Stofl and Vladimir select an arbitrary one (you cannot influence their choice). It also can happen that the distance between two villages is equal to .
Prove, that for all distances, Stofl can never be faster as Vladimir. Formally: Given villages (), where each village is connected with every other village with integer distances . Show that the distance of mouse Stofl is greater or equal than the distance that mouse Vladimir travels.
Or, regarding the previous subtasks, that there is no example for .
The proof is not obvious. You cannot simply write that it is clear, because Vladimir always takes the smaller distances. Maybe Vladimir is in a position where he can only take very expensive paths. Try to write your arguments clear and precise. We don’t expect a strict mathematical proof, but the arguments have to be founded.
Lemmas
To help you, we have divided the proof into lemmas. You don’t have to follow this scheme, it should only help you to proceed further.
Lemma 1: Distances are either of length 0 (blue) or 1 (red). The red lines meet in exactly one point.
- Lemma 1: Villages are either in distance 1 or 0. Additionally, all connections of cost 1 join in a single point (see image).
- Lemma 2: Villages are either in distance 1 or 0. The restrictions of the previous lemma don’t hold anymore.
- Lemma 3: There is no restriction to the distances between villages (this is the full proof).
For each solved lemma, you get 20 points. To proof lemma 3, you can assume lemma 2 (and you get the points for lemma 3, but not for lemma 2). Conversly, you can proof the lemma 2 directly (without lemma 1) and get also points for lemma 1.
More precise: If you solve lemma directly, you automatically have solved lemmas . If you solve , you can assume lemmas , but they don’t get solved automatically. For each solved lemma, you get up to 20 points.
The contest is over, you can no longer submit.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Racing
Each year, the grand cheese prix takes place in Kazan (Russia). This is one of the largest formula 1 races in the mouse world. Mouse Stofl will travel to the IOI in Kazan together with the Swiss delegation in order to participate in this prestigeous race. Help him to win it.
The game
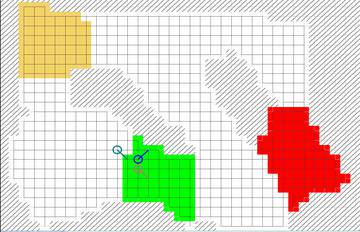
One full run of the game
Each player handles one vehicle and the game takes place on a map consisting of squares. A game consists of several rounds. In each round, each player announces which square he would like to move to. After all players have announced their moves, they all move simultaneously. There is one constraint though: the velocity vector (the vector between the two preceding positions, or, in other words, the vector between the last and the next position) may only change by 1 in each direction. On the racing track, there are multiple different checkpoints, which must all be visited in an arbitrary order before the goal can be reached (the squares where the goal is located may, of course, be visited earlier, but the game does not complete in this case.) Multiple players can be on the same square at the same time.
Additionally, each player is given one cheese as well as one mouse trap. Players passing near cheese will be unable to change their velocity vectors for a small time, while the mouse trap brings all players near to it to a full stop.
Some notes about cheese and mouse traps (in the following, both referred to as “objects”):
- The objects can be placed at an arbitrary time and they become active at the end of the current round, after all players have been moved.
- The objects are active during one round only, after that, they will be removed.
- Arbitrarily many objects can be placed in one round, as long as the maximum number for the entire game is not surpassed.
- Each player is given 1 cheese and 1 mouse trap per game.
- The objects can be placed on an arbitrary field, it does not have to be nearby the player.
- The objects affect all players, even the one who placed them.
- The objects affect players located up to a distance of 2 squares. Imagine a square with side length 5, where the object is located on the middle field. All fields in this square are affected by the object.
- The cheese influences affected players during two rounds. Assuming the cheese is placed in round , and player A is in the square affected by the cheese, the player will be unable to change their velocity vector in rounds and .
- At certain places in the game server and its documentation, the terms “Bomb” and “Freezer” appear. Those refer to mouse traps and cheese respectively.
One round is organized as follows:
- All players indicate the square they would like to move to. They must meet the constraints on their velocity vectors. Players may also place objects at this time.
- All players are moved to their indicated field.
- The placed objects are evaluated and their effects on players are applied.
If a player moves outside the racing track, they are moved back to the checkpoint last visited, and the velocity vector is reset to 0/0. It is allowed to move outside the track, i.e. a blocked square, or a square outside the map (even though it appears unclear why one would want to do this…).
What is a vector
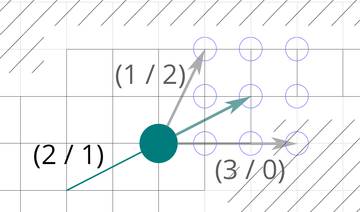
In each turn, the initial vector (2 / 1) can be changed
by one in each dimension.
If you have already been taught about vectors in school, you may skip this part.
A vector can be thought of as an arrow which points in a certain direction. In order to represent such a direction, multiple numbers are taken together to form a new object, called a vector. In our case, we have two dimensions. The cars have a position on the X-axis (“left-right”) as well as on the Y-Axis (“up-down”). Therefore, the vector we use for the velocity also consists of two numbers. This vector tells us, by how many fields the car moves per round. The first number describes the change on the X-axis, the second number describes the change on the Y-axis.
For the Y-axis, there are two conventions: either the numbers increase upwards, or downwards. In school, you will probably learn the first variant, which is probably more intuitive: the elevation above sea level grows upwards, as do e.g. numbers on floors in high buildings. In informatics, the second variant is also common though. E.g. the position of a window is represented as a distance to the left upper corner of the screen (and therefore, the number for the Y-axis grows as the window moves further down). This is sensible e.g. in a text editor, where line numbers grow downwards. We will use the second variant, such that numbers grow downwards.
Example: Assuming the car is located at position (5 / 8) (i.e. 5 squares right of the origin and 8 squares below the origin. The origin is located at the upper left corner of the map). If the car currently is moving at a velocity of (2 / 3), it will be located at position (7 / 11) in the next round. The arrow represented by the velocity vector points 2 squares to the right and 3 squares downwards. If one moves this arrow to the current position, it will point right to the target sqaure (7 / 11).
You are able to change the velocity vector by 1 in each direction and each round. I.e. if you are traveling with a velocity vector of (2 / 3), you have 9 possible ways to choose your velocity:
- Maintaining the velocity: (2 / 3)
- Changing the velocity on the X-axis by 1: (1 / 3), (3 / 3)
- Changing the velocity on the Y-axis by 1: (2 / 2), (2 / 4)
- Changing the velocity by 1 on both axes: (1 / 2), (1 / 4), (3 / 2), (3 / 4)
Input and Output
The program will be restarted for each game. Communication is done over standard I/O. In order to be able to solve the task, you will need a program provided by us, which you can download at the end of this description. In this section, everything that is important about handling this program will be explained.
On the first line there are given (width of the map), (height of the map) and (number of players)
lines consisting of characters each follow. The -th character in the -th line corresponds to the element at position (i / j). The characters have the following meaning.
| Character | Meaning |
|---|---|
| . | Free square |
| # | Wall |
| = | Start |
| $ | Goal |
| a to z | Checkpoint |
After reading this information, the player prints X Y, describing his desired starting position (an arbitrary field which is marked with ).
At the begin of each round, the server will print a single line with 1. P lines follow, describing the current state of the other players:
N X Y VX VY B F
The ID of the player (N, the players are numbered from 0 to P-1, your program always has the ID 0), the current position (X Y) the current velocity (VX VY) as well as the number of remaining mouse traps (B) and cheese (F). The players are sorted by ID.
On the next line follow B F, the numbers of placed mouse traps as well as cheese. There follow B + F lines containing X Y N, describing the position of one object as well as the ID of the player who has placed it. The first B lines describe mouse traps, the remaining ones describe cheese.
After that, the program should print the desired action(s). First, if desired, it should place mouse traps and cheese with B X Y or F X Y. The last line describes the desired square with M X Y. (I.e. the vehicle should move to position (X / Y)). Here, the velocity vector may change by at most 1 in each direction. If the old position is (AX / AY), the new position is (NX / NY) and the original velocity vector is (VX / VY), we have: |(NX - AX) - VX| <= 1 and |(NY - AY) - VY| <= 1.
Caution: If the vehicle is influenced by cheese or a mouse trap, it may differ from the one expected.
Example
> 50 20 2 > ################################################## > #######..................................######### > ####......................................aa###### > ###.........##........#############....aaaaaaa#### > ###===.....##########################aaaaaaaaaa### > ###=======###########################aaaaaaaaa.### > ###....===###########################aaaaa......## > ###......############################a.........### > ###.....###############################.........## > ###.....###############################........### > ##$$$$$$################################.......### > ##$$$$$$################################.......### > ##$$$$$$################################.......### > ##.......##############################........### > ###.......#########################bbbb........### > ##.........######................bbbbbbb.......### > ##................................bbbbbbb....##### > ###................................bbbbbbb..###### > ##########..................#######bbbbbbb.####### > ################################################## < 3 4 > 1 > 0 3 4 0 0 1 1 > 1 3 4 0 0 1 1 > 0 0 < M 3 3 > 1 > 0 3 3 0 -1 1 1 > 1 3 3 0 -1 1 1 > 0 0 < M 4 3 > 1 > 0 4 3 1 0 1 1 > 1 4 3 1 0 1 1 > 0 0 < M 4 2 > 1 > 0 4 2 0 -1 1 1 > 1 4 2 0 -1 1 1 > 0 0 < B 37 18 < M 4 3 > 1 > 0 4 3 0 1 0 1 > 1 4 3 0 1 1 1 > 1 0 > 37 18 0 < M 4 5 > 1 > 0 4 5 0 2 0 1 > 1 4 5 0 2 1 1 > 0 0 ... < M 7 8 > 1 > 0 7 8 0 2 0 1 > 1 15 9 0 2 1 0 > 0 0 < M 6 10 > 0
Subtask 1: Find a Path (20 Points)
You play alone and you should find the goal.
You should solve the task using a program, which computes the path at runtime (i.e. you are expected not to determine a specific path by hand and just save it into your program.) Play one game with your program and upload the generated file replay.txt. At the end of this description you can find an explanation on how to run your program.
Use this map as your input.
Constraints
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 2: Find the Optimal Path (30 Points)
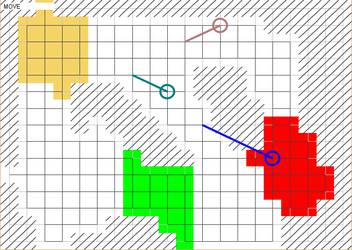
A small map, for which it is feasible to find an optimal path.
You are playing alone, and you should find the shortest path you can. If is the optimal number of rounds for the given map, and your program uses rounds, you will be awarded points (where ).
You must solve the task using a program, which computes the path at runtime (i.e. you are expected not to determine a specific path by hand and just save it into your program.)
Du musst die Aufgabe mit einem Programm lösen, welches den Weg zur Laufzeit berechnet (d.h. Du darfst nicht von Hand einen Weg bestimmen und diesen fest in deinem Programm speichern). Play one game with your program and upload the generated file replay.txt.
Use this map as your input.
Constraints
The contest is over, you can no longer submit. But you can still solve the task (‘upsolve’ it), and check your solution here.
If the time expires, or you don’t get full points, you can try again by downloading a fresh input.
You can directly run C++ solutions in your browser. For other languages, you need to download the input and manually run your solution. Please note that running in the browser is slower than running natively.
Do not navigate away while your solution is running.
Subtask 3: Creativity Tourney (50 Points)
You play against the other participants of the SOI. At SOI day, your programs will compete against each other in a tourney, in order to determine the best programs. You will be awarded points according to the ranking.
Constraints
Definitive Submission
Upload the source code which is to be used for the final ranking & the tourney at SOI day. You may submit up to three programs, the best one will be used for the ranking. Bundle these programs in a zip archive and submit that.
The contest is over, you can no longer submit.
Additional Maps
Notes
For interactive tasks, it is important that you flush the output buffer after each round, to ensure that the output becomes visible to the server.
Use the following commands:
- C/C++: fflush(stdout);
- C++: cout << flush; (not necessary, if right after printing, a read happensx)
- Pascal: flush(output);
- There are similar commands in other languages.
Furthermore, when reading the input, it is important that your program does not wait for more characters that the server provides as input. Especially spaces or line endings in C format strings are a common source of mistakes. For example, if you have read the last variable in the input using “scanf("%d ",&x);”, the scanf-function will wait for the next character which is not either a space or line ending. However, you will only be provided such a charater when you will already have provided your next move. In order to solve this, use “scanf("%d", &x);”, i.e., no non-printable characters afer the “%d”.
Sample-Bots, Server and Visualisation
During the first round, we will provide the following materials:
- Sample-bots in different programming languages
- A server-program which you can use to let your own program compete against your own and other programs as well as against yourself.
- A visualisation showing simulated games.
- Additional Maps to test your bots.
You can download them here.
Short Manual
In order to execute the server, you need Java (version 7 or higher). The server program itself is located in the file server.jar, the remaining files are configuration files, example maps as well as sample-bots. You can start the server via double click on server.jar, where you will have a menu, or via the console (Windows: Cmd, Map: Terminal, Linux: Shell) with arguments. Using the first variant, you do not have quite all the possible options, but this should be sufficient for testing a bots, or generating the log files for the first two subtasks. If you start the program via the console, use the command java --jar server.jar arguments, where arguments are replaced by the desired arguments. A detailed explanation of all possible arguments as well as further information are provided in the file usage.md included in the server download.
To play a game by hand, use the mouse to select a square and the keys M (move), B (set a mouse trap) and F (place cheese) to select the next action. With PageUp and PageDown you can zoom and using the arrow keys you can move the view.
Don’t hesitate to ask us any question about this task, programming or the website via email (info@soi.ch).
Ranking
| Rank | Username | Total (600) | cablecar (100) | gotthard (100) | matryoshka (100) | waterslide (100) | salesman (100) | racing (100) |
|---|---|---|---|---|---|---|---|---|
| loading ... |
Case #1: For the first cable car, the slope between the first and the second pillar is 2, which is also the case between the second and the third pillar. The slope does not change. Hence the view can be enjoyed.
Case #2: For the second cable car, the slope between the first to the second pillar is 2 as well, but the slope between the second to the third pillar is 5. As the slope changes, the view cannot be enjoyed optimally.